P5014 Water Triangle (Modified Version)
Background
This triangular diagram looks really nice.
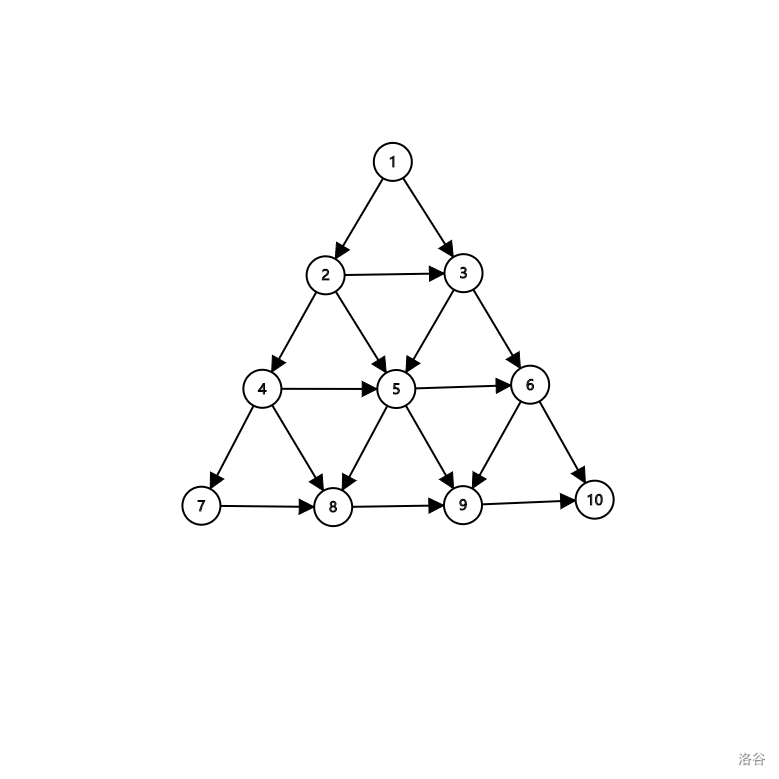
This is a ${\rm 4}$-order triangular diagram.
Description
Now we define a triangular diagram as shown above.
Please find the number of ways to walk from node $1$ to node $u$ in an infinitely large triangular diagram.
There are $T$ queries.
Input Format
The first line contains a positive integer $T$.
The second line contains $T$ positive integers $u_i$.
Output Format
Output $T$ lines, each containing a positive integer, which is the answer modulo $998244353$.
Explanation/Hint
${\rm Subtask\ 1(10\ pts)}$: $1 \leq T \leq 100, \qquad 1 \leq u_i \leq 55$.
${\rm Subtask\ 2(20\ pts)}$: $1 \leq T \leq 100, \qquad 1 \leq u_i \leq 12502500$.
${\rm Subtask\ 3(30\ pts)}$: $1 \leq T \leq 100, \qquad 1 \leq u_i \leq 500000500000, \qquad u_i=\frac{x \times (x + 1)}{2}$.
${\rm Subtask\ 4(40\ pts)}$: $1 \leq T \leq 100, \qquad 1 \leq u_i \leq 500000500000$.
Translated by ChatGPT 5