P5018 [NOIP 2018 Junior] Symmetric Binary Tree

NOIP 2018 Junior Group T4.

A rooted tree with node weights is called a symmetric binary tree by Xuanxuan if it satisfies the following conditions: 1. It is a binary tree. 2. If we swap the left and right subtrees of every node in the tree, then in the new tree and the original tree, the structures at corresponding positions are the same and the node weights are equal. In the figure below, the number inside each node is the weight, and the $id$ outside each node indicates the node index.  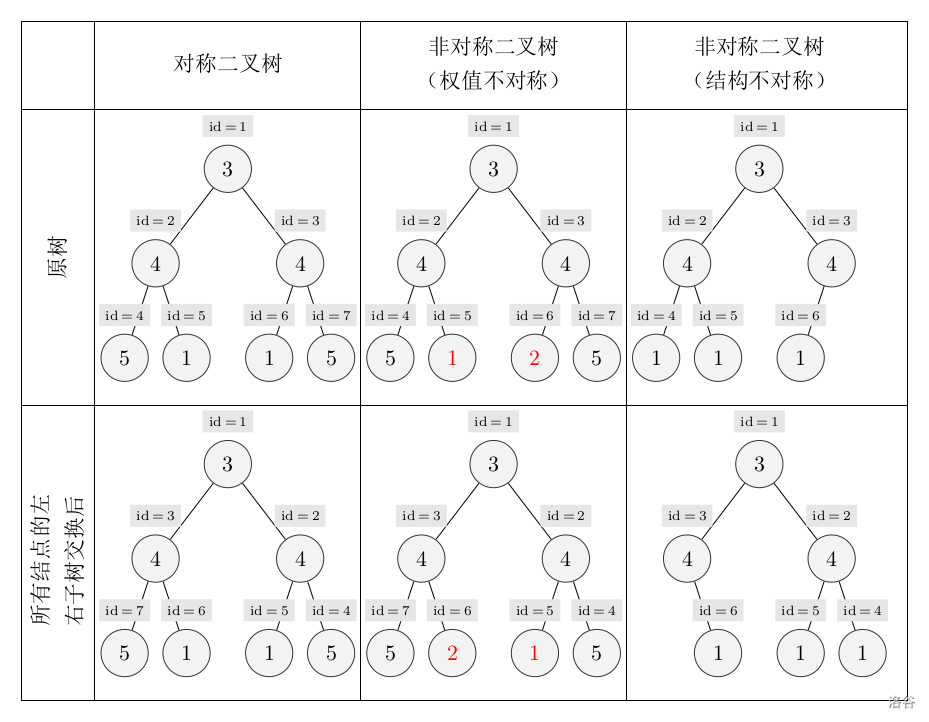Now you are given a binary tree. You need to find a subtree that is a symmetric binary tree and has the maximum number of nodes. Output the number of nodes in that subtree. Note: A tree with only the root is also a symmetric binary tree. In this problem, a “subtree” rooted at node $T$ means the binary tree formed by node $T$ and all of its descendants.

The first line contains a positive integer $n$, representing the number of nodes in the given tree. The node indices are $1 \sim n$, and node $1$ is the root. The second line contains $n$ positive integers separated by spaces. The $i$-th positive integer $v_i$ represents the weight of node $i$. The next $n$ lines each contain two integers $l_i, r_i$, representing the indices of the left and right children of node $i$, respectively. If the left/right child does not exist, it is represented by $-1$. The two numbers are separated by a space.

Output one line containing an integer, representing the maximum number of nodes among all symmetric binary subtrees of the given tree.

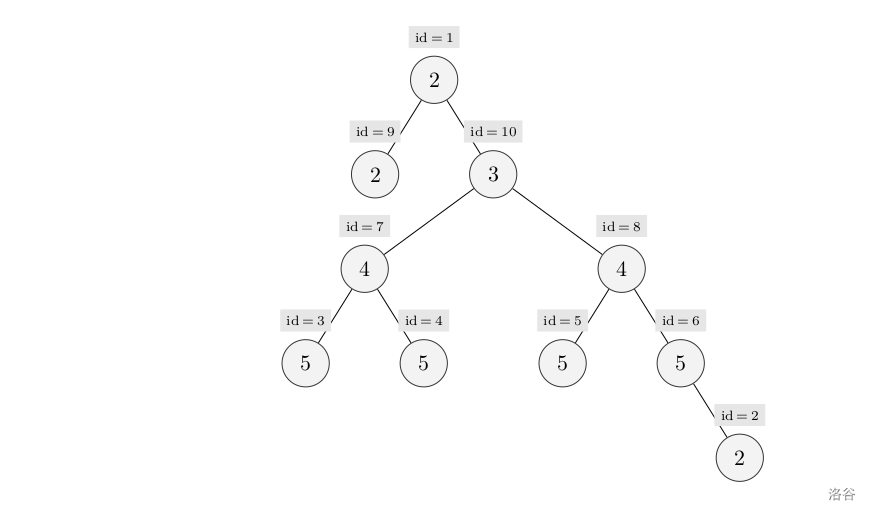
**Sample 1 Explanation**  The largest symmetric binary subtree is the subtree rooted at node $2$, and the number of nodes is $1$. **Sample 2 Explanation**  The largest symmetric binary subtree is the subtree rooted at node $7$, and the number of nodes is $3$. **Constraints** There are $25$ test points in total. $v_i \le 1000$. - Test points $1 \sim 3$, $n \le 10$. It is guaranteed that all nodes in the left subtree of the root have no right child, and all nodes in the right subtree of the root have no left child. - Test points $4 \sim 8$, $n \le 10$. - Test points $9 \sim 12$, $n \le 10^5$. It is guaranteed that the input is a “full binary tree”. - Test points $13 \sim 16$, $n \le 10^5$. It is guaranteed that the input is a “complete binary tree”. - Test points $17 \sim 20$, $n \le 10^5$. It is guaranteed that all node weights in the input tree are $1$. - Test points $21 \sim 25$, $n \le 10^6$. In this problem, the following definitions apply: Level: The level of nodes starts from the root. The root is on level 1, and the children of the root are on level 2. The level of any node in the tree equals the level of its parent node plus $1$. Depth of a tree: The maximum level of nodes in the tree is called the depth of the tree. Full binary tree: Suppose the depth of a binary tree is $h$, and the binary tree has $2^h - 1$ nodes. Then it is a full binary tree.  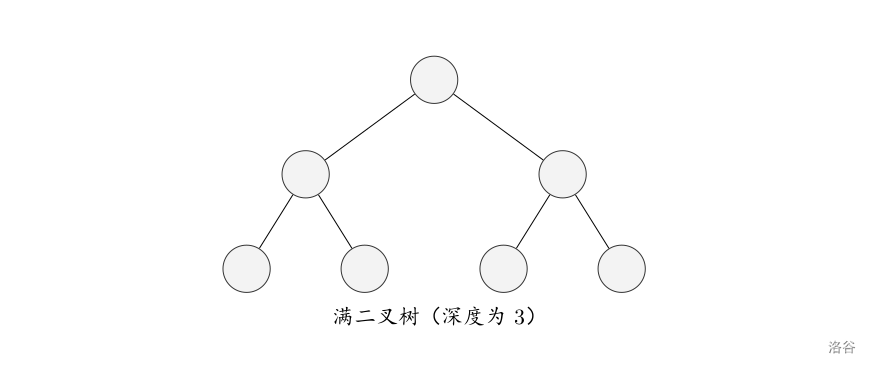Complete binary tree: Suppose the depth of a binary tree is $h$. Except for level $h$, the number of nodes on all other levels reaches the maximum. All nodes on level $h$ are continuously packed to the far left. Then it is a complete binary tree.  Translated by ChatGPT 5