P5020 [NOIP 2018 Senior] Currency System

NOIP 2018 Senior D1T2.

In the netizens’ kingdom, there are $n$ different denominations of currency. The denomination of the $i$-th currency is $a[i]$. You may assume that there are infinitely many bills of each denomination. For convenience, we denote the currency system with $n$ types of currency and denomination array $a[1..n]$ as $(n,a)$. In a perfect currency system, every non-negative integer amount $x$ should be representable. That is, for every non-negative integer $x$, there exist $n$ non-negative integers $t[i]$ such that the sum of $a[i] \times t[i]$ equals $x$. However, in the netizens’ kingdom, the currency system may be imperfect, meaning there may exist an amount $x$ that cannot be represented by the system. For example, in the currency system $n=3$, $a=[2,5,9]$, the amounts $1,3$ cannot be represented. Two currency systems $(n,a)$ and $(m,b)$ are equivalent if and only if, for any non-negative integer $x$, either $x$ can be represented by both systems, or $x$ cannot be represented by either of them. Now the netizens plan to simplify the currency system. They want to find a currency system $(m,b)$ such that $(m,b)$ is equivalent to the original currency system $(n,a)$, and $m$ is as small as possible. They hope you can help complete this difficult task: find the minimum $m$.

The first line of the input file contains an integer $T$, the number of test cases. Then $T$ test cases are given in the following format. The first line of each test case contains a positive integer $n$. The next line contains $n$ positive integers $a[i]$ separated by spaces.

The output file contains $T$ lines. For each test case, output one positive integer per line, representing the minimum $m$ among all currency systems $(m,b)$ that are equivalent to $(n,a)$.

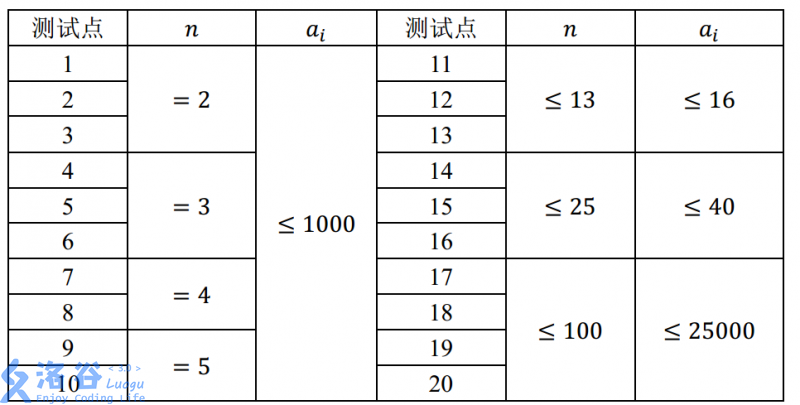
In the first test case, the currency system $(2, [3,10])$ is equivalent to the given currency system $(n, a)$. It can be verified that there is no equivalent currency system with $m < 2$, so the answer is $2$. In the second test case, it can be verified that there is no equivalent currency system with $m < n$, so the answer is $5$. 【Constraints】  For $100\%$ of the testdata, $1 \le T \le 20$, and $n,a[i] \ge 1$. Translated by ChatGPT 5