P5021 [NOIP 2018 Senior] Track Construction

City C is going to host a series of car races. Before the races, it is necessary to build $m$ race tracks in the city. City C has $n$ intersections, numbered $1,2,\ldots,n$. There are $n-1$ bidirectional roads suitable for building tracks, and each road connects two intersections. The $i$-th road connects intersections $a_i$ and $b_i$, and its length is $l_i$. Using these $n-1$ roads, you can reach every other intersection from any starting intersection. A track is a sequence of pairwise distinct roads $e_1,e_2,\ldots,e_k$, such that you can start from some intersection, then pass through roads $e_1,e_2,\ldots,e_k$ in order (each road is used exactly once, and turning back is not allowed), and finally arrive at another intersection. The length of a track is the sum of the lengths of all roads it passes through. For safety, each road may be used by at most one track. The track construction plan has not been decided yet. Your task is to design a construction plan so that, among the $m$ tracks built, the shortest track is as long as possible (that is, maximize the minimum track length among the $m$ tracks).

The first line contains two positive integers $n,m$ separated by spaces, representing the number of intersections and the number of tracks to be built. The next $n-1$ lines each contain three positive integers $a_i,b_i,l_i$, describing the two intersections connected by the $i$-th road and the road length. It is guaranteed that any two intersections are mutually reachable via these $n-1$ roads. Adjacent numbers in each line are separated by one space.

Output one line containing one integer, representing the maximum possible value of the minimum track length.

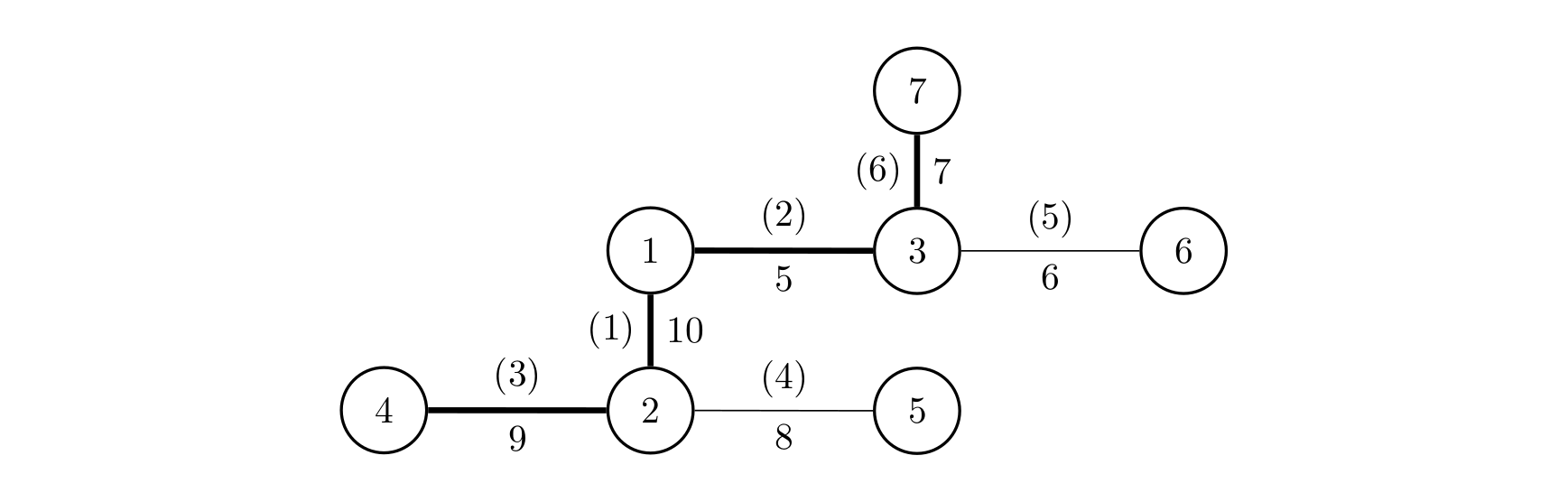
[Explanation for Sample 1] All intersections and the roads suitable for building tracks are shown in the figure below:  The number in parentheses beside a road is the road index, and the number not in parentheses is the road length. You need to build $1$ track. You can build a track that goes through roads $3,1,2,6$ (from intersection $4$ to intersection $7$). Then the track length is $9 + 10 + 5 + 7 = 31$, which is the maximum among all plans. 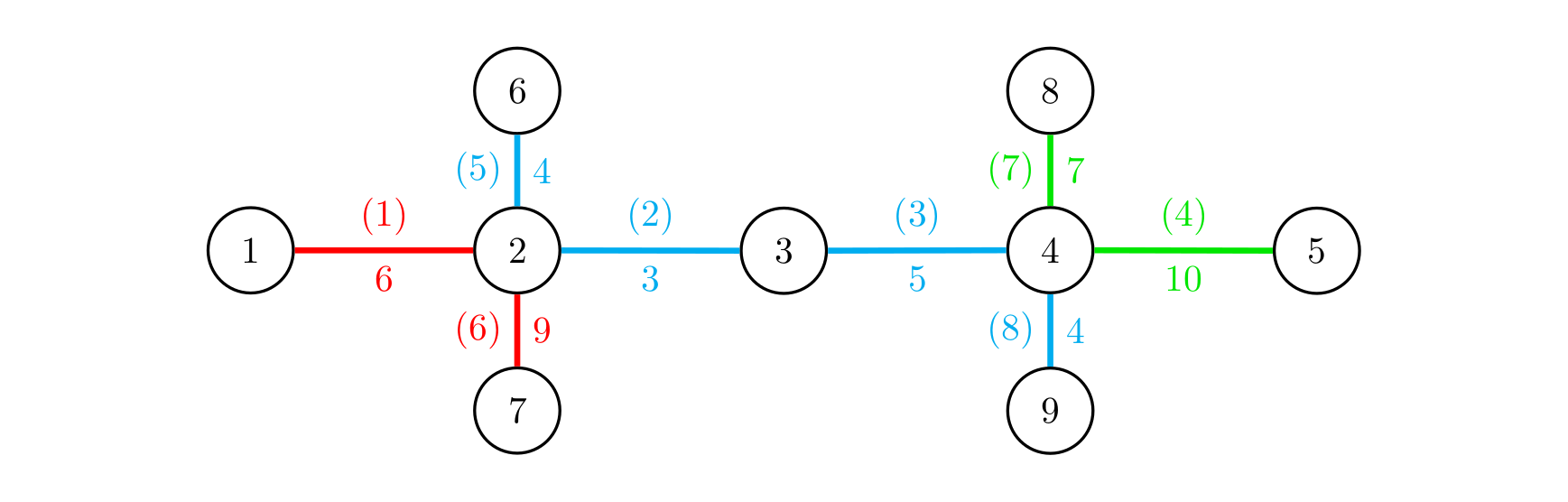[Explanation for Sample 2] All intersections and the roads suitable for building tracks are shown in the figure below:  You need to build $3$ tracks. You can build the following $3$ tracks: 1. A track that goes through roads $1,6$ (from intersection $1$ to intersection $7$), with length $6 + 9 = 15$; 2. A track that goes through roads $5,2,3,8$ (from intersection $6$ to intersection $9$), with length $4 + 3 + 5 + 4 = 16$; 3. A track that goes through roads $7,4$ (from intersection $8$ to intersection $5$), with length $7 + 10 = 17$. The minimum track length is $15$, which is the maximum among all plans. ### Constraints The ranges and characteristics of all testdata are shown in the table below: | Test Point ID | $n$ | $m$ | $a_i=1$ | $b_i=a_i+1$ | Branching $\le 3$ | |:-:|:-:|:-:|:-:|:-:|:-:| | $1$ | $\le 5$ | $=1$ | No | No | Yes | | $2$ | $\le 10$ | $\le n-1$ | No | Yes | Yes | | $3$ | $\le 15$ | $\le n-1$ | Yes | No | No | | $4$ | $\le 10^3$ | $=1$ | No | No | Yes | | $5$ | $\le 3\times 10^4$ | $=1$ | Yes | No | No | | $6$ | $\le 3\times 10^4$ | $=1$ | No | No | No | | $7$ | $\le 3\times 10^4$ | $\le n-1$ | Yes | No | No | | $8$ | $\le 5\times 10^4$ | $\le n-1$ | Yes | No | No | | $9$ | $\le 10^3$ | $\le n-1$ | No | Yes | Yes | | $10$ | $\le 3\times 10^4$ | $\le n-1$ | No | Yes | Yes | | $11$ | $\le 5\times 10^4$ | $\le n-1$ | No | Yes | Yes | | $12$ | $\le 50$ | $\le n-1$ | No | No | Yes | | $13$ | $\le 50$ | $\le n-1$ | No | No | Yes | | $14$ | $\le 200$ | $\le n-1$ | No | No | Yes | | $15$ | $\le 200$ | $\le n-1$ | No | No | Yes | | $16$ | $\le 10^3$ | $\le n-1$ | No | No | Yes | | $17$ | $\le 10^3$ | $\le n-1$ | No | No | No | | $18$ | $\le 3\times 10^4$ | $\le n-1$ | No | No | No | | $19$ | $\le 3\times 10^4$ | $\le n-1$ | No | No | No | | $20$ | $\le 5\times 10^4$ | $\le n-1$ | No | No | No | Here, “Branching $\le 3$” means that each intersection is connected to at most $3$ roads. For all data, $2 \le n \le 5\times 10^4, \ 1 \le m \le n − 1,\ 1 \le a_i,b_i \le n,\ 1 \le l_i \le 10^4$. # Input Format The first line contains two positive integers $n,m$ separated by spaces, representing the number of intersections and the number of tracks to be built. The next $n-1$ lines each contain three positive integers $a_i,b_i,l_i$, describing the two intersections connected by the $i$-th road and the road length. It is guaranteed that any two intersections are mutually reachable via these $n-1$ roads. Adjacent numbers in each line are separated by one space. # Output Format Output one line containing one integer, representing the maximum possible value of the minimum track length. # Hint Translated by ChatGPT 5