P5022 [NOIP 2018 Senior] Travel

NOIP 2018 Senior D2T1.

Xiao Y is an OIer who loves traveling. She comes to Country X and plans to visit every city. Xiao Y learns that there are $m$ undirected roads among the $n$ cities in Country X. Each undirected road connects two cities. There are no two roads connecting the same pair of cities, and there is no road connecting a city to itself. Also, starting from any city, one can reach any other city through these roads. Xiao Y can only travel from one city to another using these roads. Xiao Y’s travel plan is as follows: she chooses any city as the starting point, and then starting from it, each time she can either choose a road connected to the current city and go to a city she has not visited before, or go back to the previous city along the road she used when she first visited the current city. When Xiao Y returns to the starting point, she may choose to end the trip or continue. Note that Xiao Y requires that in her plan, every city must be visited. To make her trip more meaningful, every time she arrives at a new city (including the starting point), she records its index. She knows this will form a sequence of length $n$. She wants this sequence to be lexicographically smallest. Can you help her? For two sequences $A$ and $B$ of length $n$, we say $A$ is lexicographically smaller than $B$ if and only if there exists a positive integer $x$ such that: - For any positive integer $1 \le i < x$, the $i$-th element $A_i$ of $A$ equals the $i$-th element $B_i$ of $B$. - The value of the $x$-th element of $A$ is smaller than that of the $x$-th element of $B$.

The input has $m + 1$ lines. The first line contains two integers $n,m(m \le n)$, separated by a space. The next $m$ lines each contain two integers $u,v (1 \le u,v \le n)$, indicating that there is a road between the cities numbered $u$ and $v$. The two integers are separated by a space.

Output one line with $n$ integers, representing the lexicographically smallest sequence. Adjacent integers are separated by a space.

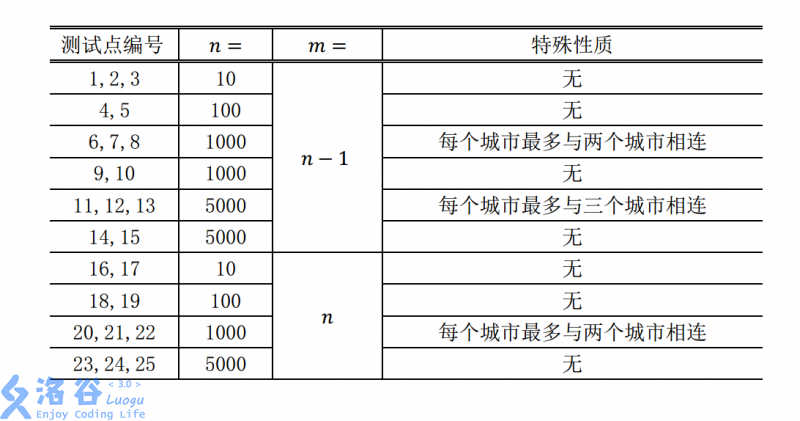
## Constraints For $100\%$ of the data and all samples, $1 \le n \le 5000$ and $m = n - 1$ or $m = n$. For different test points, the constraints are as follows:  Translated by ChatGPT 5