P5023 [NOIP 2018 Senior] Number Filling Game

NOIP 2018 Senior D2T2.

Xiao D really likes playing games. One day, he was playing a number filling game. The board of this game is an $n \times m$ rectangular grid. The player needs to fill each cell in the grid with a number (either $0$ or $1$), and the filling must satisfy some constraints. We describe these constraints in detail below. For convenience, we first give some definitions: - We use the row and column coordinates of each cell to represent a cell, i.e., (row, column). Note: both row and column coordinates start from $0$. - A valid path $P$: A path is valid if and only if: 1. The path starts from the top-left cell $(0,0)$ of the grid and ends at the bottom-right cell $(n - 1,m - 1)$; 2. Along this path, each move can only go from the current cell to the adjacent cell on its right, or from the current cell to the adjacent cell below it. For example, in the rectangle below, only two paths are valid: $P_1$: $(0,0)\to (0,1)\to (1,1)$ and $P_2$: $(0,0) \to (1,0) \to (1,1)$.  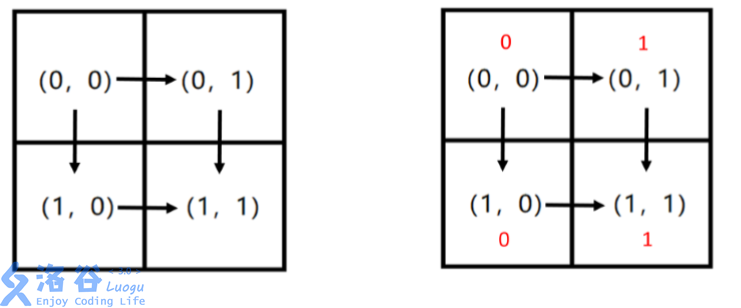For a valid path $P$, we can represent it with a string $w(P)$ of length $n + m - 2$, which contains only the characters $\texttt R$ or $\texttt D$. The $i$-th character records how the $i$-th step of path $P$ moves. $\texttt R$ means moving to the adjacent cell on the right of the current cell, and $\texttt D$ means moving to the adjacent cell below the current cell. For example, for path $P_1$ in the figure above, $w(P_1) = \texttt {RD}$; for the other path $P_2$, $w(P_2) = \texttt {DR}$. Also, if we concatenate, in order, the numbers filled in each cell visited by a valid path $P$, we obtain a $01$ string of length $n + m - 1$, denoted by $s(P)$. For example, if we fill $0$ in cells $(0,0)$ and $(1,0)$, and fill $1$ in cells $(0,1)$ and $(1,1)$ (as the red numbers in the figure), then for path $P_1$ we get $s(P_1) = 011$, and for path $P_2$ we get $s(P_2) = 001$. The game requires Xiao D to find a way to fill $0$ and $1$ such that for any two paths $P_1$, $P_2$, if $w(P_1) > w(P_2)$, then it must hold that $s(P_1) \le s(P_2)$. We say that string $a$ is smaller than string $b$ if and only if $a$ is lexicographically smaller than $b$. The definition of lexicographical order is given in detail in Problem 1. However, finding just one method does not satisfy Xiao D’s curiosity. Xiao D wants to know how many different ways the game can be played, that is, how many filling methods satisfy the requirement. Xiao D is not strong enough, so he hopes you can help solve this problem: how many ways of filling $0$ and $1$ can satisfy the requirement? Since the answer may be very large, you need to output the answer modulo $10^9 + 7$.

The input consists of one line containing two positive integers $n,m$, separated by a space, representing the size of the rectangle. Here $n$ is the number of rows of the grid, and $m$ is the number of columns of the grid.

Output one line containing a positive integer, representing how many ways of filling $0$ and $1$ can satisfy the requirement. Note: output the result modulo $10^9+7$.

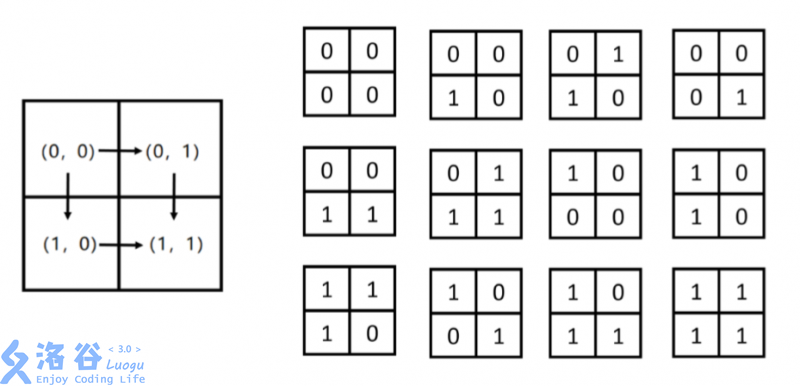
**Sample Explanation**  **Constraints** | Test Point ID | $n\le$ | $m\le$ | | :-----------: | :-----------: | :-----------: | | $1\sim 4$ | $3$ | $3$ | | $5\sim 10$ | $2$ | $10^6$ | | $11\sim 13$ | $3$ | $10^6$ | | $14\sim 16$ | $8$ | $8$ | | $17\sim 20$ | $8$ | $10^6$ | Translated by ChatGPT 5