P5031 Ponzi Scheme
Background
As everyone knows, a Ponzi scheme is a scam that uses new debt to pay off old debt, hiding the truth that the business has already gone downhill, while maintaining fake growth.
Description
The Ponzi scheme originated from a man named Charles Ponzi. In 1919, he created a mysterious-looking fake financial plan and sold it to the public. In this way, he cheated tens of thousands of long-necked giraffes in Boston, taking nearly 15 million US dollars from them.
Charles Ponzi’s scam plan has two parts. The first time, he showed his startup plan to $K_1$ giraffes, and asked each giraffe for an investment of 10,000 yuan. The second time, he showed his startup plan to $K_2$ giraffes. Since the second time needed to cover the losses from the first time, he asked each giraffe for an investment of 20,000 yuan.
Now, Charles Ponzi has $K_1$ amounts of 10,000 yuan and $K_2$ amounts of 20,000 yuan. He hopes to spend the money in a specific way to avoid being tracked by the IRS. Every day, he will choose two amounts of money, and spend 10,000 yuan from each of them. To further reduce suspicion, the two amounts he chooses each day will not repeat any pair chosen before. He wants to know: after spending all the money, how many different sets of plans are there, **that is, there is no order inside a plan set, and the days are also unordered**.
For example, if on the first day he chooses money from giraffes $(1,2)$, then on the second day he cannot spend money from giraffes $(1,2)$ again, but he can take money from a giraffe pair such as $(2,3)$ or $(1,3)$.
Output the number of plans modulo $10^9+7$.
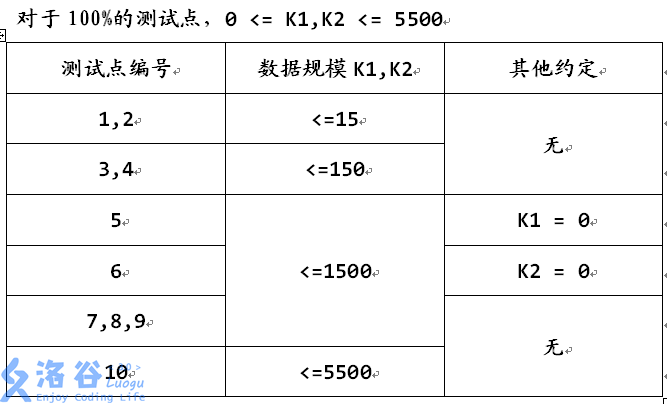
Input Format
One line with two positive integers, $K_1,K_2$.
Output Format
One line with one positive integer, the number of plans.
Explanation/Hint
##### Sample Explanation
Suppose giraffes $1,2$ each gave 10,000 yuan, and giraffes $3,4$ each gave 20,000 yuan.
Plan 1 is the plan set ${(1,3),(3,4),(2,4)}$.
Plan 2 is the plan set ${(1,4),(3,4),(2,3)}$.
Translated by ChatGPT 5