P5032 Experience

[In-contest Q&A](https://www.luogu.org/discuss/show/80694). **The simplified version has been updated, and the time limit has been changed to 500 ms.** Save up enough experience to enchant~~ Steve often runs into problems in Minecraft: He wants to repair $n$ enchanted books, and the level of each book is $a_i$. He never really understands the anvil repair and experience mechanisms, so he searched for some information on the wiki:  —The figure shows the relationship between experience and level. After seeing this figure, he thought: the higher my level is, the more experience I need. So if my level is just enough for anvil repairing, wouldn’t I spend the least experience? He continued searching and attached the anvil mechanism below, asking you to help him solve the problem.

#### Prior Work Penalty Whether it is renaming, repairing, or combining, the experience cost increases due to the item’s previous operations on an anvil. This extra cost is called the “prior work penalty”. For an item that has never been put on an anvil, the prior work penalty is $0$. After each anvil operation on an item (excluding renaming), its prior work penalty is multiplied by $2$ and then increased by $1$. Therefore, after $N$ operations, the prior work penalty is $2^N-1$. After $6$ operations, the prior work penalty is $63$ levels, and in survival mode no further repairing or enchanting can be done. After $31$ operations, the penalty level is $2147483647$, and no operations can be done in any mode. When combining two items, the player suffers the prior work penalties of both items at the same time. The prior work penalty of the combined item is calculated based on the higher one of the two items. For example, combining two items with prior work penalties of $3$ and $15$ will add an extra penalty cost of $18$ levels, and the resulting item’s penalty is $31$ ($15 \times 2+1$). The prior work penalty even applies to items that do not wear out, such as enchanted books. Therefore, combining $4$ Fortune I enchanted books will produce a Fortune III enchanted book with a prior work penalty of $3$. |Total operation count|Penalty| |:--:|:--:| |$0$|$0$| |$1$|$1$| |$2$|$3$| |$3$|$7$| |$4$|$15$| |$5$|$31$| Repairing items using the crafting grid removes all prior work penalties, but it also removes all enchantments. #### Combining Items In the anvil interface, the item in the first slot/on the left is called the target item; the item in the second slot/on the right is called the sacrifice item—it will disappear after combining. If the sacrifice item has enchantments, the anvil will also try to merge the sacrifice item’s enchantments into the target item. Regardless of whether the enchantments on the target item actually change, the anvil will charge the player a level cost based on the enchantments on both the target item and the sacrifice item. For each enchantment on the sacrifice item, if the target item also has the same enchantment: - If the sacrifice item’s enchantment level is higher, the target item’s enchantment level will increase to the sacrifice item’s level. - If the sacrifice item’s enchantment level is the same, the target item’s enchantment level will increase by $1$ level, unless it is already at the maximum level. - If the sacrifice item’s enchantment level is lower, the target item’s enchantment level does not change. The total cost of combining items is the sum of the following costs: 1. The sum of the target item’s and the sacrifice item’s prior work penalties. 2. If renaming is also performed, an additional renaming cost is added. 3. If the target item’s durability is not full, it costs $2$ levels for repairing. 4. If the sacrifice item has enchantments, an enchanting cost is added. 5. If the sacrifice item is an enchanted book, there is no repairing cost. The anvil will attempt to merge the book’s enchantments into the target item. Renaming the target item can also be performed at the same time. In this case, the enchanting cost is usually less than the cost of combining two similar items. —Adapted from mcwiki with minor edits. #### Simplified Version You are given enchanted books. Only books of the same level can be combined. The cost of combining is the sum of the two books’ accumulated costs. The accumulated cost of the resulting book becomes $2$ times the maximum accumulated cost before combining, plus $1$. Find the highest level and the minimum cost (the highest level is the primary objective). Steve is using cheats, so the highest level is unlimited. Now you are given $n$ enchanted books, and each book has its level $a_i$. Ask how to obtain the maximum level $x$ of an enchanted book. On this basis, compute the minimum level cost $y$ to combine it (we assume the initial prior work penalty of each book is $1$). Steve is lazy. He does not want to read the above text; he only wants you to write a program to compute $x$ and $y$. But to prevent it from being spread, he only asks you to output $k$, the multiplicative inverse of $x$ modulo $y$. If it does not exist, output $-1$.

The first line contains an integer $n$. In the next $n$ lines, each line contains an integer $a_i$, representing the initial level of each enchanted book. The data is not guaranteed to be sorted.

Output one integer $k$, representing the multiplicative inverse of $x$ modulo $y$. If it does not exist, output $-1$. PS: The multiplicative inverse $k$ can also be understood as: $k$ is the smallest positive integer such that $kx \equiv 1 \pmod y$.

### Sample Explanation The first sample: Combine two level $1$ books: cost $2$ experience, accumulated cost becomes $3$; Then combine two level $2$ books: cost $3+1=4$ experience, accumulated cost becomes $7$; Then combine two level $3$ books: cost $7+1=8$ experience, accumulated cost becomes $15$; Finally combine two level $4$ books: cost $15+1=16$ experience, accumulated cost becomes $31$. Total experience cost: $2+4+8+16=30$, maximum level: $5$. For the first sample: $x=5,y=30$. For the second sample: $x=3,y=10$. 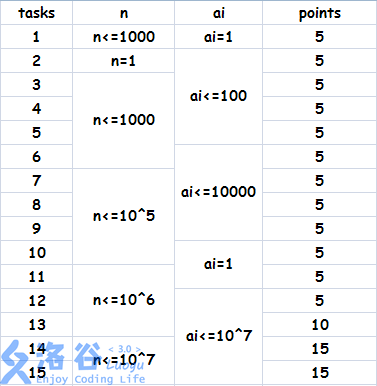### Constraints  The data is guaranteed to be random, and $x,y,k$ are within the range of `long int`. ### Friendly Reminder The input size of this problem is large, so please use a fast input method. Here is an example of fast input (requires including the header ``): ```cpp #include inline void read(int &x){ char ch=getchar();x=0; while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0',ch=getchar(); } ``` Translated by ChatGPT 5