P5039 [SHOI2010] Minimum Spanning Tree

Secsa has recently become very interested in the minimum spanning tree problem. He already knows that to find the minimum spanning tree of an undirected graph with $n$ vertices and $m$ edges, there is the Krustal algorithm and another Prim algorithm. He also knows that a graph may have several different minimum spanning trees. 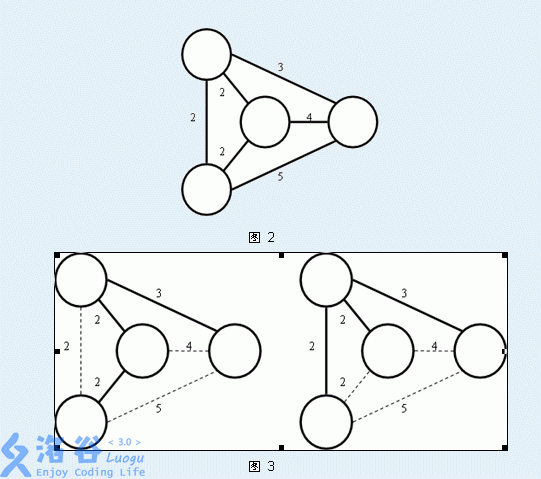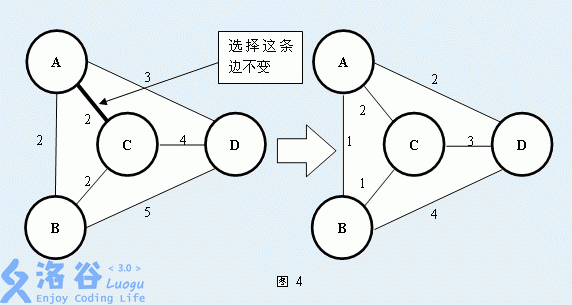For example, all the graphs shown in Figure 3 below are minimum spanning trees of the undirected graph in Figure 2:  Of course, these are not what you need to solve today. Secsa wants to know, for a certain edge $AB$ in an undirected graph, at least how much cost is needed to guarantee that edge $AB$ is in the minimum spanning tree of this undirected graph. To make sure that edge $AB$ must be in the minimum spanning tree, you may perform operations on this undirected graph. A single operation is defined as follows: first choose an edge $P1P2$ in the graph, then decrease the weight of every edge except this one by $1$. Figure 4 shows one such operation: 

The first line of the input file contains three positive integers $n, m, Lab$, which represent the number of vertices, the number of edges, and the index of the edge $AB$ that must appear in the minimum spanning tree. The next $m$ lines describe the undirected edges with indices $1, 2, 3 \ldots m$ in order, one edge per line. Each line contains three integers $x, y, d$, meaning this edge connects vertices $x$ and $y$, and its weight is $d$. The input guarantees that $1 \leq x, y \leq N$, $x \neq y$, and the undirected graph is connected.

The output file contains only one line with one integer: the minimum number of operations required to ensure that the edge with index $Lab$ must appear in the minimum spanning tree.

Constraints: $1 \leq N \leq 500$, $1 \leq M \leq 800$, $1 \leq d < 10^6$. Translated by ChatGPT 5