P5045 [SCOI2003] Spider Problem

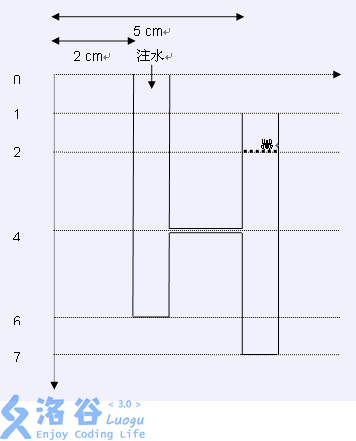
There is a set of pipes and a spider $\text{Willy}$, as shown in the figure below. All pipes are open at the top and sealed at the bottom. Each pipe has a diameter of $1cm$. The connections between two pipes have infinite capacity, but their volume can be ignored.  Above the first pipe there is a water source, from which water keeps flowing downward at a rate of $0.25cm^3$ per second. Since the cross-sectional area of a pipe is $0.25cm^2$, when filling only one pipe, the water level rises by $1cm$ per second. According to physics, during the first $2$ seconds, the water flows into the bottom of the left pipe; during seconds $[3,5]$, it flows into the right pipe; during seconds $[6,9]$, it flows into both pipes at the same time (although the total flow rate is unchanged, because two pipes are filled simultaneously, the rising speed in each pipe is only $0.5cm$ per second), and then it reaches the spider. Given the positions of the connections between pipes and the position of the spider $\text{Willy}$, find the time when the water level touches $\text{Willy}$. Assume the spider’s actual position is slightly higher than the given one. Therefore, if the spider is at position $n=4$ in the left pipe, the answer should be $5$ seconds. This is because after the first two seconds the water level seems to touch $\text{Willy}$, but it is actually slightly below $\text{Willy}$.

All positions are represented by ordered pairs $(x, y)$, where the $y$ coordinate increases from top to bottom, and the $x$ coordinate increases from left to right. Therefore, the top-left corner is $(0,0)$. All other coordinate values are integers between $0$ and $100$. The first line contains an integer $p(1

Output only one integer: the time when the water level touches $\text{Willy}$. If the water level can never touch $\text{Willy}$, output $-1$.

Translated by ChatGPT 5