P5088 Rectangle
Background
Xiao Ben did very well on the monthly exam. As a reward, the teacher gave him a laser pointer.
Description
However, the teacher never gives Xiao Ben a prize for free. He told Xiao Ben that the angle of reflection equals the angle of incidence, and asked him to solve the following problem.
Given a rectangle whose length-to-width ratio is $N:M$. A laser beam is emitted from the top-left corner, and the angle between the beam and the side of length $N$ is $\zeta°$ ($0\le \zeta° \le 90$). It also satisfies $\cot \zeta° = A:B$. Find the minimum number of reflections needed for the beam to enter (after reflections) any one of the four corners again.
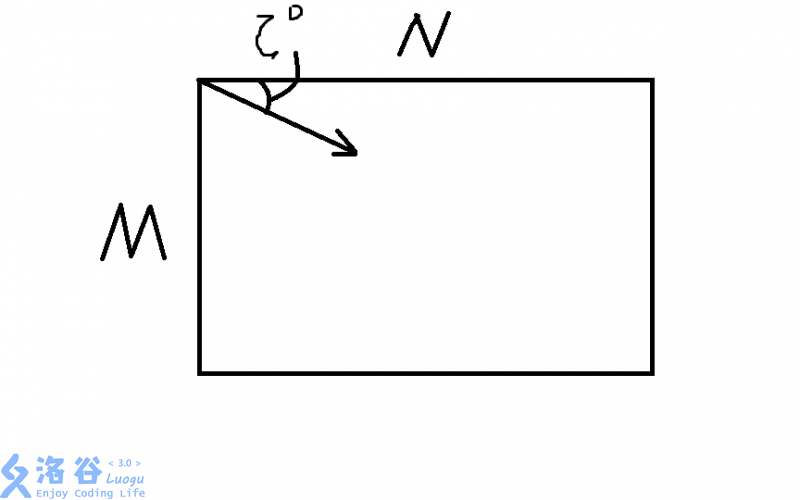
Input Format
Two lines.
The first line contains two numbers $N$ and $M$, representing the ratio of the length to the width.
The second line contains two numbers $A$ and $B$, representing $\cot\zeta°$.
Output Format
One positive integer, representing the minimum number of reflections needed.
Explanation/Hint
For $10\%$ of the testdata, $A=B=1$.
For another $10\%$ of the testdata, $N=M$.
For $50\%$ of the testdata, $0\le A,B,M,N\le10^5$.
For $100\%$ of the testdata, $0\le A,B,M,N\le10^{10}$.
Translated by ChatGPT 5