P5089 [eJOI 2018] Periodic Table of Elements

**This problem is translated from [eJOI2018](http://ejoi2018.org/) Problem D “Chemical table”.**

Professors at Innopolis University are working hard on studying the periodic table of elements. They know that there are $n \times m$ elements, forming a matrix with $n$ rows and $m$ columns. Research shows that if there is an element $A$ in the periodic table, element $B$ is in the same column as it (but $A$ and $B$ cannot be in the same row), and element $C$ is in the same row as it (but $A$ and $C$ cannot be in the same column), then scientists can use these three elements to produce a sample of a fourth element $D$ by nuclear fusion. Element $D$ is in the same row as $B$ and in the same column as $C$. 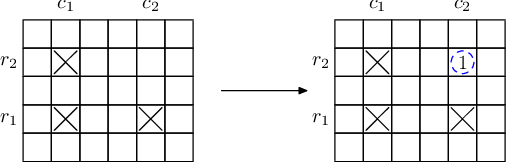In short, if there are samples of three elements located at $(r_1, c_1),\ (r_1, c_2),\ (r_2, c_1)$ in the periodic table (where $r_1 \neq r_2, c_1 \neq c_2$), then a sample at $(r_2, c_2)$ can be produced, as shown in the figure:  **Note: The samples used in nuclear fusion do not disappear; they can take part in later reactions. Samples obtained from reactions can also take part in reactions.** They have already obtained samples of $q$ elements. To collect samples of all elements, they will buy some samples and then use nuclear fusion to produce the remaining ones. Please find the minimum number of element samples they need to buy.

The first line contains $3$ integers $n, m, q \ (1 \le n, m \le 2 \times 10^5, 0 \le q \le \min \{n \times m, 2 \times 10^5\})$. The next $q$ lines each contain $2$ integers $r_i, c_i \ (1 \le r_i \le n, 1 \le c_i \le m)$. It is guaranteed that all given elements are distinct.

Output one integer, the minimum number of element samples that need to be bought.

### Sample Explanation #### Notes In each sample explanation, there are two matrices. The first shows the initial state (where **crosses mark the elements that already have samples**). The second shows the final state when all samples have been collected (where **blue circles represent samples obtained by nuclear fusion, the number inside a blue circle is the order in which it was obtained, and red circles represent purchased samples**). #### Sample Explanation 1 With the three given elements, a sample of the fourth element can be obtained.  #### Sample Explanation 2 Since the given elements are only in one row, nuclear fusion cannot be used, so the remaining two element samples can only be purchased.  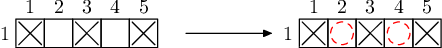#### Sample Explanation 3 The method for collecting all elements is not unique; the following is one possible method. In this method, element $(4, 2)$ can only be obtained after purchasing a sample of element $(4, 1)$ and obtaining a sample of element $(1, 1)$ from reactions.  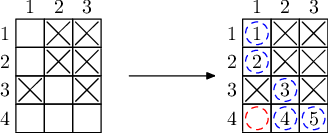--- ### Subtasks **Note: You will receive the score for a subtask if and only if you pass all test points in that subtask.** |Subtask ID|Score|$n$|$m$|$q$| |:-:|:-:|:-:|:-:|:-:| |$1$|$10$|$n=2$|$m=2$|$0 \le q \le 4$| |$2$|$17$|$1 \le n \le 2$|$1 \le m \le 20$|$0 \le q \le 20$| |$3$|$8$|$1 \le n \le 20$|$1 \le m \le 20$|$q=0$| |$4$|$20$|$1 \le n \le 20$|$1 \le m \le 20$|$0 \le q \le 400$| |$5$|$30$|$1 \le n \le 1 \times 10^4$|$1 \le m \le 1 \times 10^4$|$1 \le q \le 1 \times 10^5$| |$6$|$15$|$1 \le n \le 2 \times 10^5$|$1 \le m \le 2 \times 10^5$|$1 \le q \le 2 \times 10^5$| Translated by ChatGPT 5