P5090 [eJOI 2018] 互素树

**本题译自 [eJOI2018](http://ejoi2018.org/) Problem E「Prime Tree」**

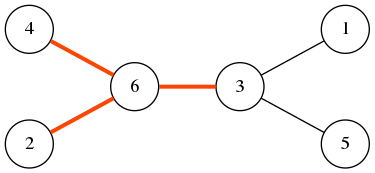
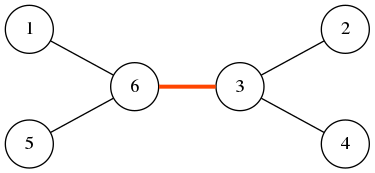
本题为提交答案，输入文件在附件中。 设有一棵有 $n$ 个结点的树，其结点编号为 $1$ 到 $n$ 。 对于其中的任意一条边 $(u, v)$ ，如果存在一个正整数 $d>1$ 满足 $ d \mid u, d\mid v$ ，我们称它为一条**坏的边**。 下图中的树有三条坏的边—— $(6, 4)$（都被 $2$ 整除）， $(2, 6)$（都被 $2$ 整除）， $(3, 6)$（都被 $3$ 整除）。  你的任务是将结点重新编号，使得图中坏的边的数量尽量少。 对于上图中的树，按照下图中的方式将结点重新编号，会只剩一条坏的边 $(3, 6)$ 。  重新编号后，坏的边越少，你的得分越高。 **这是一道提交答案题。你应当下载输出文件，然后在本地运行你的程序，将输出结果上传**。当然，在洛谷上你可以直接提交你的程序。

每个测试点中有多组测试数据。 第一行，一个整数 $T$，表示测试数据组数。 每组测试数据共 $n$ 行，其中 $n$ 表示树的结点个数。 第一行，一个整数 $n$； 接下来 $n-1$ 行，每行两个整数 $u$ 和 $v\ ( 1 \le u, v \le n)$，表示一条边 $(u,v)$ 。 **每个输入文件中，每棵树的结点个数相同。**

对于每组测试数据，输出一行 $n$ 个整数，表示原先编号为 $1$ 到 $n$ 的结点的新编号。 **每个结点的编号必须不同，也就是说同一组测试数据中输出的 $n$ 个整数必须互不相同。**

### 计分方式 对于每个测试点，设所有树的总边数为 $M=T \times (n-1)$，你的输出中坏的边数为 $X$，记 $R=\dfrac{X}{M}$ ，你的得分与 $R$ 的关系如下： |$R$|得分|$R$|得分| |:-:|:-:|:-:|:-:| |$0.33 < R \le 0.4$|$1$|$0.01 < R \le 0.05$|$6$| |$0.26 < R \le 0.33$|$2$|$0.005 < R \le 0.01$|$7$| |$0.19 < R \le 0.26$|$3$|$0.001 < R \le 0.005$|$8$| |$0.12 < R \le 0.19$|$4$|$0 < R \le 0.001$|$9$| |$0.05 < R \le 0.12$|$5$|$R=0$|$10$| 当 $R > 0.4$ 时，不能得分。 **对于所有的测试点，保证存在 $X=0$ 的输出。** --- ### 样例解释 注意样例中给出了两种合法的输出，为了方便，下称输出 1 和 输出 2。 第一组测试数据已经在题目描述中讨论过。输出 1 中有一条坏的边 $(3, 6)$，输出 2 中没有坏的边。 第二组测试数据中，输出 1 和输出 2 都没有出现坏的边。 样例中，$M=2 \times 5=10$。 对于输出 1，$X=1, R=\dfrac{1}{10}=0.1$，该输出将得到 $5$ 分。 对于输出 2，$X=0, R=\dfrac{0}{10}=0$，该输出将得到 $10$ 分。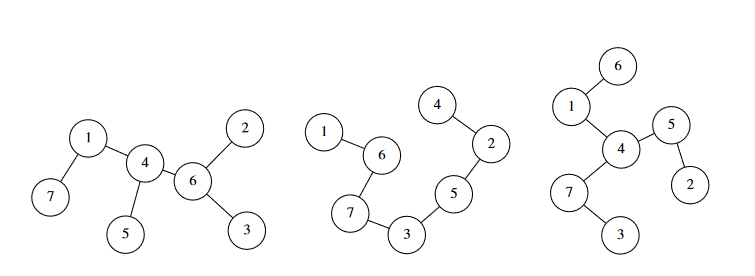 --- ### 数据范围和限制 #### 数据限制 - 对于测试点 1 （输入 `01`），$T=3, n=7$，三棵树分别如下所示：  - 对于测试点 4 至 8 （输入 `04` 至 `08`），输入数据有特殊性质（如叶子结点较多，是二叉树等），且这些具有特殊性质的树在各个测试点中输入数据均匀分布。 - 对于其他测试点，数据为随机生成。 #### 数据范围 |测试点编号|1|2|3|4|5|6|7|8|9|10| |:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:| |文件名|`01`|`02`|`03`|`04`|`05`|`06`|`07`|`08`|`09`|`10`| |$T$|$3$|$100$|$100$|$500$|$200$|$50$|$10$|$5$|$2$|$1$| |$n$|$7$|$10$|$30$|$100$|$500$|$2000$|$10000$|$20000$|$50000$|$100000$|