P5090 [eJOI 2018] Coprime Tree

**This problem is translated from [eJOI2018](http://ejoi2018.org/) Problem E "Prime Tree".**

This is an output-only problem. The input files are provided in the attachments. There is a tree with $n$ nodes, numbered from $1$ to $n$. For any edge $(u, v)$, if there exists a positive integer $d > 1$ such that $d \mid u$ and $d \mid v$, then we call it a **bad edge**. In the tree shown below, there are three bad edges: $(6, 4)$ (both divisible by $2$), $(2, 6)$ (both divisible by $2$), and $(3, 6)$ (both divisible by $3$).  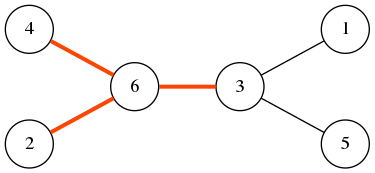Your task is to renumber the nodes so that the number of bad edges is as small as possible. For the tree above, if you renumber the nodes as in the figure below, there will be only one bad edge left, $(3, 6)$.  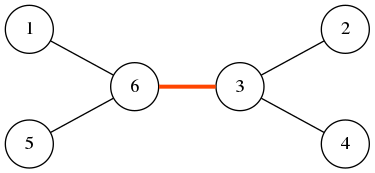After renumbering, the fewer bad edges you have, the higher your score will be. **This is an output-only problem. You should download the output file, then run your program locally and upload the output result.** Of course, on Luogu you may also submit your program directly.

Each test point contains multiple groups of testdata. The first line contains an integer $T$, the number of testdata groups. Each group of testdata has $n$ lines in total, where $n$ is the number of nodes in the tree. The first line contains an integer $n$. The next $n - 1$ lines each contain two integers $u$ and $v \ (1 \le u, v \le n)$, representing an edge $(u, v)$. **In each input file, all trees have the same number of nodes.**

For each group of testdata, output one line with $n$ integers, representing the new labels of the nodes originally labeled from $1$ to $n$. **All node labels must be different. That is, the $n$ integers you output for the same group of testdata must be pairwise distinct.**

### Scoring For each test point, let the total number of edges in all trees be $M = T \times (n - 1)$. Let the number of bad edges in your output be $X$, and define $R = \dfrac{X}{M}$. Your score as a function of $R$ is as follows: |$R$|Score|$R$|Score| |:-:|:-:|:-:|:-:| |$0.33 < R \le 0.4$|$1$|$0.01 < R \le 0.05$|$6$| |$0.26 < R \le 0.33$|$2$|$0.005 < R \le 0.01$|$7$| |$0.19 < R \le 0.26$|$3$|$0.001 < R \le 0.005$|$8$| |$0.12 < R \le 0.19$|$4$|$0 < R \le 0.001$|$9$| |$0.05 < R \le 0.12$|$5$|$R = 0$|$10$| When $R > 0.4$, you get no score. **For all test points, it is guaranteed that an output with $X = 0$ exists.** --- ### Sample Explanation Note that the sample provides two valid outputs. For convenience, call them Output 1 and Output 2. The first group of testdata has already been discussed in the statement. In Output 1 there is one bad edge $(3, 6)$, while in Output 2 there are no bad edges. In the second group of testdata, neither Output 1 nor Output 2 contains any bad edges. In the sample, $M = 2 \times 5 = 10$. For Output 1, $X = 1, R = \dfrac{1}{10} = 0.1$, so this output gets $5$ points. For Output 2, $X = 0, R = \dfrac{0}{10} = 0$, so this output gets $10$ points. --- ### Constraints and Limits #### Limits - For test point 1 (input `01`), $T = 3, n = 7$. 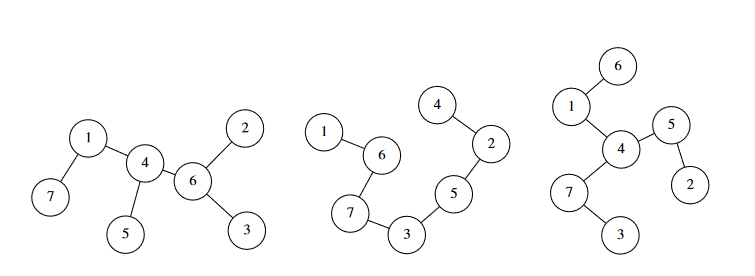The three trees are as follows:  - For test points 4 to 8 (inputs `04` to `08`), the input has special properties (for example, many leaf nodes, being a binary tree, etc.), and trees with these special properties are evenly distributed within each test point. - For the other test points, the data is randomly generated. #### Constraints |Test Point|1|2|3|4|5|6|7|8|9|10| |:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:| |Filename|`01`|`02`|`03`|`04`|`05`|`06`|`07`|`08`|`09`|`10`| |$T$|$3$|$100$|$100$|$500$|$200$|$50$|$10$|$5$|$2$|$1$| |$n$|$7$|$10$|$30$|$100$|$500$|$2000$|$10000$|$20000$|$50000$|$100000$| Translated by ChatGPT 5