P5100 [JOI 2017 Final] Soccer / Soccer

**This problem is translated from [JOI 2017 Final](https://www.ioi-jp.org/joi/2016/2017-ho/) T4「[サッカー](https://www.ioi-jp.org/joi/2016/2017-ho/2017-ho.pdf) / [Soccer](https://www.ioi-jp.org/joi/2016/2017-ho/2017-ho-en.pdf)」.** > The sentence “Assume that while the ball is rolling it can pass through other players” was added by me for strictness without changing the original testdata. The original statement did not mention this. If the ball stops when it hits other players, the solution seems to be different. You are the manager of a famous soccer club in the JOI league. The club has $N$ players, numbered $1 \ldots N$. The players train hard every day, aiming for the league championship. The soccer field can be seen as a rectangle with width $W$ meters and height $H$ meters. The width is parallel to the east-west direction, and the height is parallel to the north-south direction. If from a point you go north $i$ meters and then go west $j$ meters and arrive exactly at the northwest corner of the field, then this point can be represented by coordinates $(i, j)$. After training, you need to collect the practice soccer ball. When you start collecting, all players are on the field. Player $i \ (1 \leqslant i \leqslant N)$ is at $(S_i, T_i)$, and the ball is at the feet of player $1$. You are standing together with player $N$ at $(S_N, T_N)$, ready to collect the ball. You will collect the ball only when the players pass the ball to $(S_N, T_N)$. You can give instructions to the players, but some operations will increase a player’s **fatigue**. A player cannot perform multiple operations at the same time. You can instruct the player who currently controls the ball to perform the following operations: - **Kick**: Choose one of the four directions (east, west, south, north), and specify a positive integer $p$. The player kicks the ball exactly $p$ meters in the chosen direction. **Assume that while the ball is rolling it can pass through other players**. The player does not move, and automatically stops controlling the ball. The player’s fatigue increases by $A \times p + B$. - **Dribble**: Choose one of the four directions (east, west, south, north). The player moves with the ball by $1$ meter in the chosen direction. The player still controls the ball. The player’s fatigue increases by $C$. - **Stop controlling the ball**: The player’s fatigue does not change. You can instruct a player who does not control the ball to perform the following operations: - **Move**: Choose one of the four directions (east, west, south, north). The player moves by $1$ meter in the chosen direction. The player’s fatigue increases by $C$. - **Take control of the ball**: The player can take control only if the ball is exactly at the player’s position, and no other player is controlling the ball. The player’s fatigue does not change. Players and the ball may move outside the field, and there may be multiple players at the same position. After a day of training, the players are very tired. You want to know the minimum possible value of the sum of fatigue increases of all players during the process of collecting the ball.

The first line contains two integers $H, W$, separated by spaces. The second line contains three integers $A, B, C$, separated by spaces. The third line contains one integer $N$. In the next $N$ lines, line $i \ (1 \leqslant i \leqslant N)$ contains two integers $S_i, T_i$, separated by spaces. The meanings of all input values are described in the statement.

One line with one integer, representing the minimum sum of fatigue increases of all players during the process of collecting the ball.

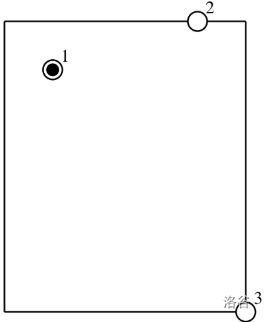
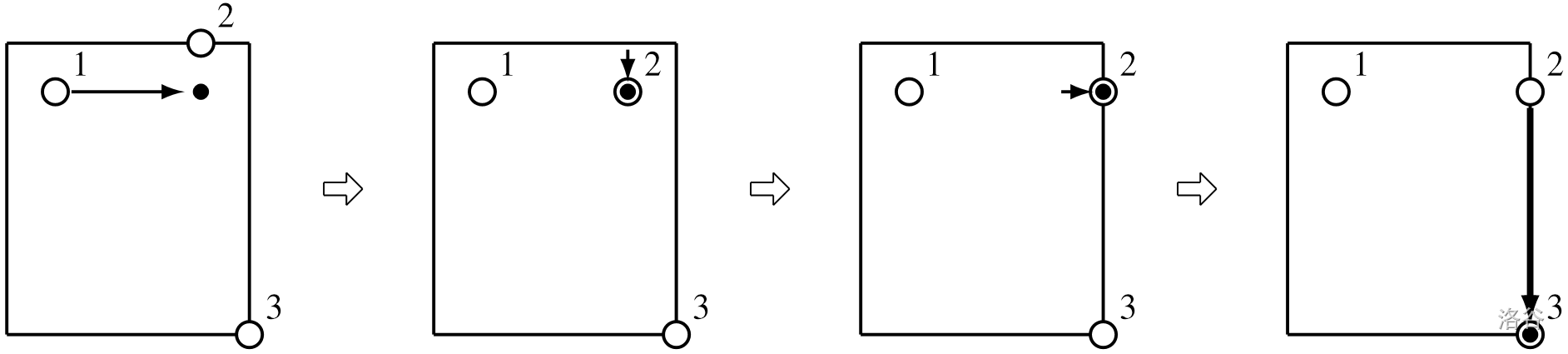
#### Sample Explanation 1 In this sample, the field, the players, and the ball are in the state shown in the figure. In the figure, the hollow circles with black outlines represent players, the solid circle represents the ball, and you are at $(6,5)$.  An optimal solution is as follows: 1. Player $1$ kicks the ball $3$ meters to the east. The fatigue increases by $1 \times 3 + 3 = 6$, and the ball moves to $(1,4)$. 2. Player $2$ moves $1$ meter to the south. The fatigue increases by another $6$. 3. Player $2$ starts controlling the ball. 4. Player $2$ dribbles $1$ meter to the east. The fatigue increases by another $6$. 5. Player $2$ kicks the ball $5$ meters to the south. The fatigue increases by $1 \times 5 + 3 = 8$, and the ball moves to $(6,5)$. At this point, the total fatigue increase is $6 + 6 + 6 + 8 = 26$. There is no better plan.  #### Sample Explanation 2 In the optimal solution, kicking is not necessary. #### Sample Explanation 4 Note that in this sample there are multiple players at the same position. #### Constraints and Hints For $5\%$ of the data, $N = 2$. For another $30\%$ of the data, $N \leqslant 1000$ and $A = 0$. For all data, $1 \leqslant H, W \leqslant 500$, $0 \leqslant A, B, C \leqslant 10^9$, $2 \leqslant N \leqslant 10^5$, $0 \leqslant S_i \leqslant H$, $0 \leqslant T_i \leqslant W \ (1 \leqslant i \leqslant N)$, $(S_1, T_1) \neq (S_N, T_N)$. Translated by ChatGPT 5