P5102 [JOI 2016 Final] Territory / Territory

**This problem is translated from [JOI 2016 Final](https://www.ioi-jp.org/joi/2015/2016-ho/index.html) T4 “[縄張り](https://www.ioi-jp.org/joi/2015/2016-ho/2016-ho.pdf)”.** There is a Cartesian coordinate plane. JOI is at $(0, 0)$. Every day, JOI follows a fixed procedure and makes one round of moves. The procedure has $N$ steps and is described by a string $S$ of length $N$. This string consists only of the uppercase letters $\texttt{E, N, W, S}$. The $i$-th character from the left, $C_i\ (1\leqslant i\leqslant N)$, indicates where JOI will move. If before executing step $i$, JOI is at $(x, y)$: * If $C_i=\texttt{E}$, JOI moves to $(x+1,y)$. * If $C_i=\texttt{N}$, JOI moves to $(x,y+1)$. * If $C_i=\texttt{W}$, JOI moves to $(x-1,y)$. * If $C_i=\texttt{S}$, JOI moves to $(x,y-1)$. On the next day, JOI starts executing the procedure from where he stopped the previous day. JOI marks $(0, 0)$ and every point he reaches after finishing each step. At the beginning, JOI has not marked any points. After $K$ days, for any integers $a, b$, if the four points $(a,b)$, $(a+1,b)$, $(a,b+1)$, $(a+1,b+1)$ have each been marked at least once, then the $1\times 1$ square with these four points as vertices belongs to JOI’s territory. Find how many territories JOI has after $K$ days.

The first line contains two integers $N, K$, separated by spaces. The second line contains a string $S$, representing JOI’s movement procedure.

Output one integer, the number of territories JOI has.

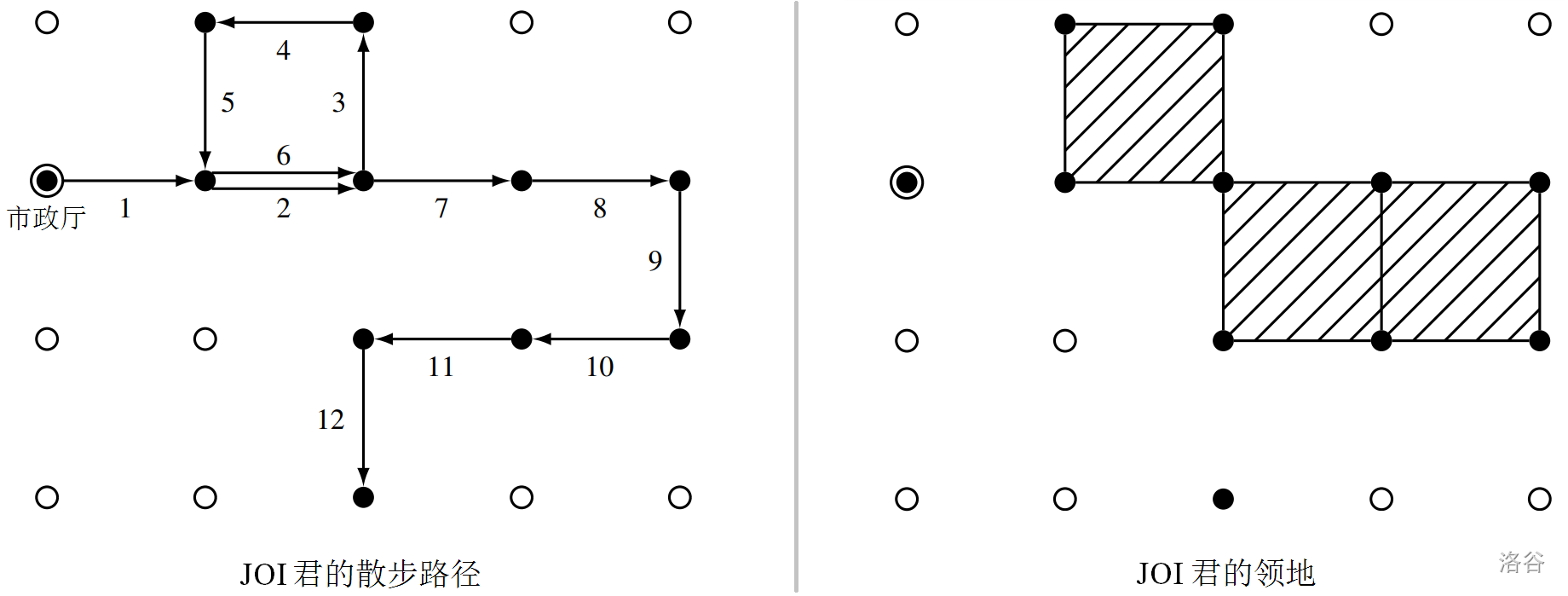
#### Sample Explanation 1  > The text in the figure is from the previous full statement, and I was too lazy to modify it. “市政厅” means $(0, 0)$, and “散步路径” means the movement path. > I did not carefully edit the image, so it may be misaligned or not symmetric. Please bear with it. #### Sample Explanation 2 The difference between Sample 2 and Sample 1 is that in Sample 2, JOI walked for two days.  #### Constraints and Hints For all testdata, $1\leqslant N\leqslant 10^5$, $1\leqslant K\leqslant 10^9$. |Subtask #|Special Constraints|Points| |-|-|-| |1|$N\leqslant 50, K = 1$|5| |2|$K = 1$|10| |3|$N\leqslant 50$|23| |4|None|62| Translated by ChatGPT 5