P5130 Pure Bullet Hell
Background
Besides the rich maze system, TODR’s bullet system is also very interesting. It not only has many gorgeous special effects, but also special attacks such as Sakuya’s rapid-fire knives and ` The World `.
Not only the player character, but enemies also have their own unique attack patterns. For example, the picture below shows Toyohime Watatsuki’s "Purifying Wind" attack pattern.
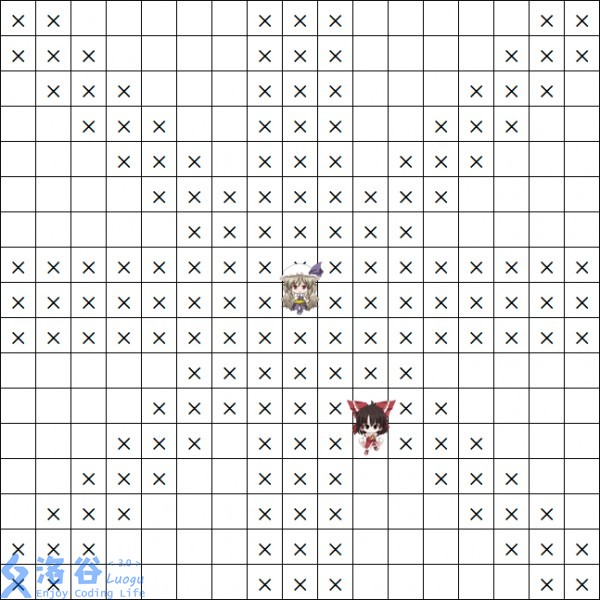
Description
After clearing the incredible maze, you fight your way smoothly to the final floor, but encounter an unprecedentedly strong enemy—Junko.
Fortunately, Junko’s bullet patterns are not as intense as in LoLK, and the room’s terrain is also quite special and can be used to your advantage.
Formally, in each turn, the action process of you and Junko is as follows.
1. You can treat the room as a square grid. The bottom-left corner has coordinates $(0,0)$, and the top-right corner has coordinates $(n,n)$. The valid positions in the room are these $(n+1)*(n+1)$ grid points. At the beginning of a turn, you will be randomly teleported to any valid position in the room.
2. After that, Junko will randomly appear at some valid position in the room. Of course, she will not appear at the same position as you.
3. Junko will fire a pure "player-targeting shot", i.e., she fires a wave of bullets toward your direction. If during the flight this wave of bullets passes through any grid point that is neither Junko’s position nor your position, then the bullet barrier on that grid point will be triggered and teleport the bullets into subspace. If this wave of bullets successfully reaches the grid point where you are, then you will take some damage.
4. Due to time rampage, the bullet damage dealt by Junko in turn $t$ can be computed as $at^{2}+bt+c$.
5. The turn ends, and the next turn begins.
After a rough estimate, you think this bullet fight with Junko will last for $k$ turns. Then, to be safe, you want to compute the total expected damage taken by the player character.
The answer may be very large or may lose precision, so you only need to take it modulo $19260817$.
Input Format
A single line contains five integers $n,a,b,c,k$, with meanings consistent with the problem statement.
Output Format
Output one integer in a single line, representing the expected total damage taken.
Explanation/Hint
Explanation for Sample $1$:
Draw a grid by hand. It is not hard to find that there are $12$ cases where Junko can hit you (place the player character first, then place Junko).
So the damage of the first wave of bullets is $1*1*1+2*1+1=4$, and the expected damage is $4*\frac{12}{16}=3$.
There is only one turn, so the answer is $3$.
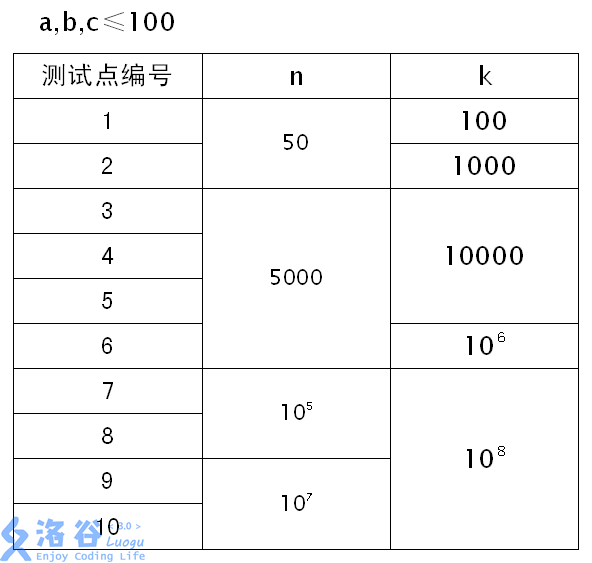
Constraints:
Translated by ChatGPT 5