P5131 Nitori Fusion

As a Roguelike game, TODR has a rich equipment system. Each piece of equipment has a unique appearance and fancy special effects. Hundreds of different “marks” with different effects, plus a complex crafting / mixing / dismantling / fusion system, make this game highly replayable. Now your equipment has been leveled to the maximum. To keep growing, you need to fuse it with other equipment. Of course, you need Kawashiro Nitori to extract the marks from your original equipment so that they can be combined with the new equipment.

It is known that the original equipment has $n$ mark slots. In each mark slot, there are infinitely many copies of one kind of mark. The value of the mark in the $i$-th slot is $a_i$. Kawashiro Nitori uses a mechanical arm to extract marks from the slots. Each time it extracts, the arm grabs downward and takes one mark from the slot directly below it. After that, the arm either moves to the right or stays in place (if it moves, it can move any number of slots). At the beginning, the arm can start at any position, but at any moment it must be above some mark slot. Kawashiro Nitori will perform $k$ grabs. After all grabs, your total reward equals the product of the values of the $k$ extracted marks. Assuming all of Kawashiro Nitori’s operations are random, what is the expected value of the reward you can obtain? Since the answer may not be an integer, you only need to output the result modulo $\text{19260817}$.

The first line contains two integers $n, k$, representing the number of mark slots and the number of grabs. The second line contains $n$ positive integers $a_i$, representing the value of the mark in each slot.

Output one integer, representing the expected reward after $k$ grabs.

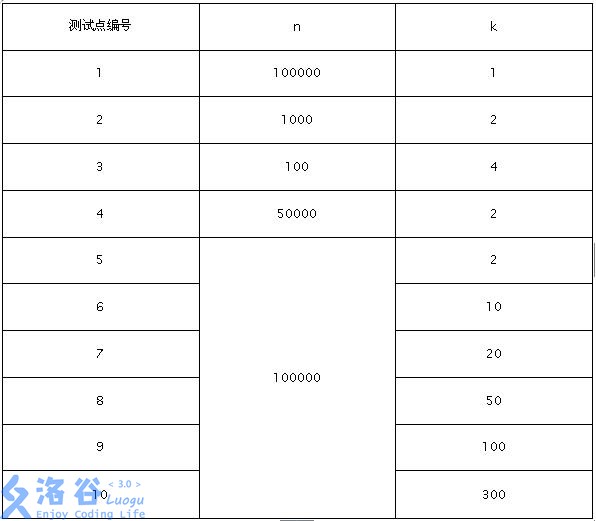
#### Sample $1$ Explanation: At the start, the mechanical arm can stay above any of the three slots. The sequence of slots from which marks are grabbed can be one of the following six types: $(1,1), (1,2), (1,3), (2,2), (2,3), (3,3)$. The rewards for each plan are $9, 3, 6, 1, 2, 4$, respectively. The average is $\frac{25}{6}$, which equals $16050685$ under $\text{mod 19260817}$. #### Constraints: $a_i < 19260817$  Translated by ChatGPT 5