P5140 Branch Pruning.

$Daleva$ $Geoge$ is a gardener who loves life.

In $Daleva$ $Geoge$'s garden, there is a tree that has not been pruned for many years. One day, guests come to $Daleva$ $Geoge$'s home. To leave a good impression, he needs to tidy up the garden, but the tree looks too unpleasant, so he must prune it carefully. This is a rooted tree with $root$ as the root, and it has $n$ nodes. $Daleva$ $Geoge$ is at the root node. He is not satisfied with the shape of some leaves and needs to cut off the extra branches. There are $S$ leaf nodes that need to be pruned. These leaf nodes have some extra branches. Each such leaf node has a weight $a_{i}$, which means how many branches on that node are not needed by $Daleva$ $Geoge$. At the same time, because the garden cannot hold these branches (otherwise it would look disharmonious), $Daleva$ $Geoge$ needs to attach these branches onto some nodes. $Daleva$ $Geoge$ has magical glue and magical scissors, so you do not need to consider the exact shape of each branch. According to $Daleva$ $Geoge$'s estimate, there are $T$ leaf nodes that need to receive these branches. These nodes have weights $b_{i}$, meaning that $b_{i}$ branches are needed to make the tree look nice. To prune the tree well, $Daleva$ $Geoge$ has to move around on the tree, cut the extra branches from those leaf nodes, and use glue to stick them onto other leaf nodes that need them. Each edge has a different length. Now, since the tree is very large, $Daleva$ $Geoge$ wants to know the minimum total distance he needs to travel to finish pruning the tree, and he also has to return to the root to climb down. Although $Daleva$ $Geoge$ has these magical tools, his pocket is limited, with capacity $G$. He cannot carry too many branches at once, i.e., no more than $G$. This makes him even less willing to think about these annoying details. Of course, $Daleva$ $Geoge$ can calculate it, but to save his energy for pruning, this hard task is left to you. $Daleva$ $Geoge$ has already told you the shape of the tree in his mind, and he will lie on a chair and watch you compute the answer.

The first line contains $3$ integers: $n,G,root$. The next $n-1$ lines describe the edges of the tree. Each line contains $3$ integers: $u,v,w$, meaning there is an edge of length $w$ between $u$ and $v$. The next line contains $2$ integers: $S,T$. The next $S$ lines each contain two integers: $x,a_{i}$, meaning node $x$ has $a_{i}$ extra branches. The testdata guarantees that $x$ is a leaf node. The next $T$ lines each contain two integers: $x,b_{i}$, meaning node $x$ needs $b_{i}$ branches. The testdata guarantees that $x$ is a leaf node. The testdata guarantees that $\sum_{i=1}^{S}a_{i}=\sum_{i=1}^{T}b_{i}$.

One line with one integer, representing the minimum total distance $Daleva$ $Geoge$ needs to travel to prune the tree and return to the root to climb down.

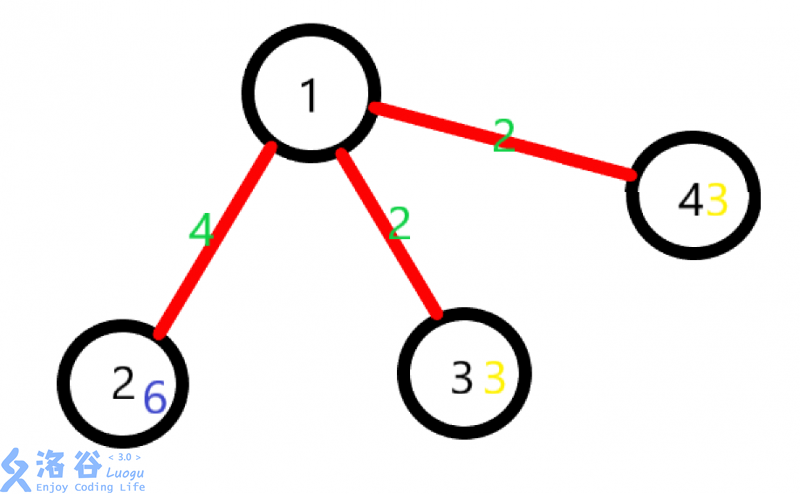
Explanation for Sample 1:  The blue numbers indicate how many extra branches there are, and the yellow numbers indicate how many branches are needed. Then the best plan is: $1→2→1→3→1→2→1→3→1→4→1→2→1→4→1$, and the answer is $40$. For $5\%$ of the testdata, it is Sample 1. For $40\%$ of the testdata, $n\leq 10,G\leq 10;w \leq 1000$. For $100\%$ of the testdata, $n\leq 40,0000,G\leq 1000;S+T\leq n;a_{i},b_{i}\leq 10^{9};w\leq 10^{9}$. The testdata guarantees that no leaf node both needs branches and has extra branches. Translated by ChatGPT 5