P5168 xtq Plays Magic Tower

**Sample explanation has been added.** When $xtq$ was in fifth grade of primary school, he became obsessed with all kinds of strange Magic Tower games. Background of the Magic Tower game: https://baike.baidu.com/item/%E9%AD%94%E5%A1%94/861619?fr=aladdin This may not be of any help for understanding the problem.

xtq is now playing a Magic Tower. This Magic Tower is very special: it is not made of square grids, but an undirected graph with $n$ vertices and $m$ edges, and there is a monster on every edge. After many obstacles, xtq has now reached a reward floor. On this floor, no monster will make xtq lose HP. However, for each monster, if xtq does not have at least a certain amount of HP, he cannot attack that monster. Each vertex also has a gem. There are many types of gems, but if xtq arrives at a vertex and he already has that type of gem, then he cannot pick it up. He now wants to know the minimum HP required to go from one vertex of the Magic Tower to another. He also wants to know, if he starts from some vertex with a certain amount of HP, how many gems he can pick up. One more thing troubles xtq a lot: due to some mysterious power, the gem types may change. It is guaranteed that if xtq has infinite HP, he can reach anywhere on this floor.

The first line contains three integers $n, m, q$, representing the number of vertices, the number of edges, and the number of operations. The second line contains $n$ integers, representing the gem type on each vertex. The next $m$ lines each contain three integers $u, v, t$, meaning there is a road between $u$ and $v$, and there is a monster on the road that requires $t$ HP to defeat. Then follow $q$ lines, each containing three integers $opt, x, y$. When $opt = 1$, change the gem at vertex $x$ to type $y$. When $opt = 2$, query the minimum HP required to go from vertex $x$ to vertex $y$. When $opt = 3$, query how many gems can be picked up if starting from vertex $x$ with HP $y$.

For each operation of type $2$ and type $3$, output one line containing the answer.

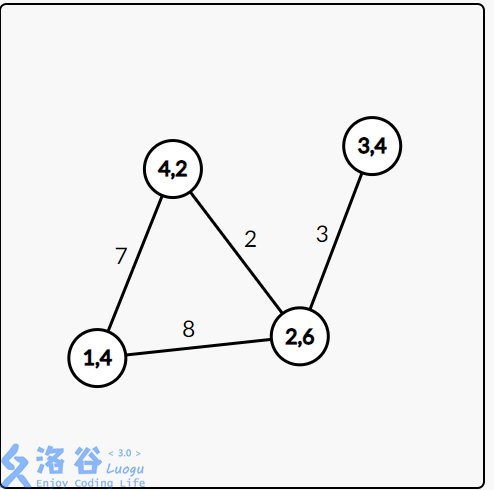
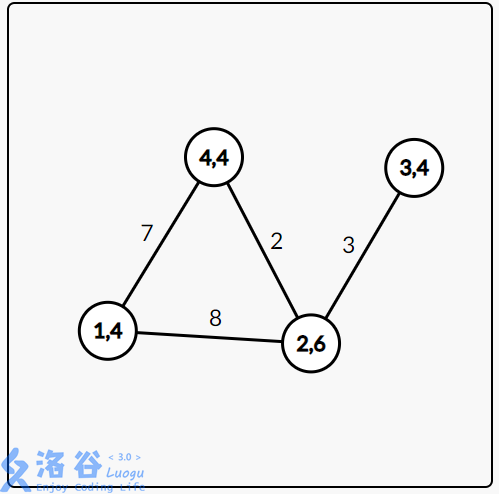
Sample explanation:  The first operation is type $3$. Starting from $4$ with $3$ HP, you can reach $\{2,3,4\}$, and the gem types you can obtain are $\{2,4,6\}$. The second operation changes the gem type of $1$ to $4$, as shown below:  The third operation is type $3$. Starting from $1$, the reachable vertices are $\{1,2,3,4\}$, and the gem types you can obtain are $\{4,6\}$. The fourth operation is type $2$. To walk from $4$ to $3$, you need at least $3$ HP. Constraints: Test Point | $n$ | $m$ | $q$ | Has modification operations ------ | ------ | --- | --- | ------ $1$ | $10$ | $20$ | $10$ | Yes $2 \sim 3$ | $1000$ | $5000$ | $5000$ | ^ $4 \sim 5$ | $8000$ | $30000$ | $20000$ | ^ $6$ | $20000$ | $100000$ | $100000$ | No $7$ | ^ | ^ | ^ | Yes $8$ | $50000$ | $200000$ | $200000$ | No $9$ | ^ | ^ | ^ | Yes $10$ | $100000$ | $300000$ | ^ | ^ For $100\%$ of the data, $n \le 100000$, $m \le 300000$, $q \le 200000$. All remaining numbers are $\le \text{intmax}$. **It is guaranteed that the query ranges are randomly generated (actually, the problem setter was too lazy to write a generator again).** Translated by ChatGPT 5