P5186 [COCI 2009/2010 #4] OGRADA

**Translated from [COCI 2010.02](http://hsin.hr/coci/archive/2009_2010/) Problem T4 “[OGRADA](http://hsin.hr/coci/archive/2009_2010/contest4_tasks.pdf)”.** Matija’s fence consists of $N$ wooden boards, numbered from left to right as $1 \ldots N$. The height of board $i$ is $h_i$, and each board has width $1\ \rm{cm}$. Matija wants to paint the boards using a roller brush of width $X\ \rm{cm}$. When using the roller, the brush must **fully** touch the fence (it cannot be partly touching and partly not), and the roller must be parallel to the ground. Therefore, each time he paints, Matija chooses $x$ consecutive boards on the fence, then “rolls” from bottom to top, until reaching the height of the shortest board among these $x$ boards. Under these rules, it is possible that some parts of the boards cannot be painted with the roller. Matija then has to “paint” the remaining parts with a toothbrush. Therefore, please help him find the minimum number of square centimeters he must paint using the toothbrush. He also wants to know, under the condition that the toothbrush-painted area is minimized, what is the minimum number of roller “rolls” needed.

The first line: $N, X$. The second line: $h_1 \ldots h_N$.

Two lines. The first line contains one integer, meaning the minimum number of square centimeters Matija must paint with the toothbrush. The second line contains one integer, meaning the minimum number of times he needs to “roll” with the roller.

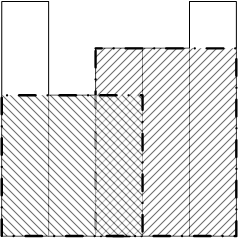
#### Sample Explanation 1  #### Constraints $1\le N\le 10^6,$ $1\le X\le 10^5,$ $1\le h_i\le 10^6$. Translated by ChatGPT 5