P5186 [COCI 2009/2010 #4] OGRADA

**译自 [COCI 2010.02](http://hsin.hr/coci/archive/2009_2010/) T4「[OGRADA](http://hsin.hr/coci/archive/2009_2010/contest4_tasks.pdf)」** Matija 的栅栏由 $N$ 条木板组成，从左到右依次编号为 $1\ldots N$。$i$ 号木板的高度为 $h_i$，每条木板的宽度是 $1\ \rm{cm}$。 Matija 想用一个宽度为 $X\ \rm{cm}$ 的滚筒刷来刷木板。使用滚筒刷时，要保证刷子**完全**接触栅栏（不能一部分接触一部分不接触）；另外，还要保证滚筒平行于地面。因此，每次涂色时，Matija 会在栅栏上选择连续的 $x$ 条木板，然后从下往上「刷」，一直刷到这 $x$ 条木板中最矮者的高度。 根据上述规则，有可能有一些木板没法用滚筒刷来刷，Matija 不得不用牙刷来「涂」剩下的部分。因此，请帮他求出他最少只需用牙刷「涂」多少平方厘米。他还想知道，在满足「涂」的面积最少的情况下，他最少要用滚筒刷「刷」多少次。

第一行：$N,X$。 第二行：$h_1\ldots h_N$。

两行。 第一行有一个整数，表示 Matija 最少需用牙刷涂多少平方厘米。 第二行有一个整数，表示最少要用滚筒刷「刷」多少次。

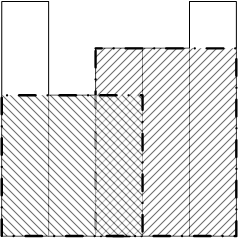
#### 样例说明 1  #### 数据范围与提示 $1\le N\le 10^6,$ $1\le X\le 10^5,$ $1\le h_i\le 10^6$.