P5210 [ZJOI2017] Segment Tree

A segment tree is a data structure that Jiu Tiao Ke Lian likes very much. It has a simple structure, good complexity, and powerful functions, so Ke Lian once spent a long time studying some properties of segment trees.

A segment tree is a data structure that Jiu Tiao Ke Lian likes very much. It has a simple structure, good complexity, and powerful functions, so Ke Lian once spent a long time studying some properties of segment trees. Recently, Ke Lian started studying segment trees again. The difference is that she focused on a more general segment tree. In a normal segment tree, for an interval $[l, r]$, we take $m = \lfloor \frac{l+r}{2} \rfloor$, and then split this interval into two sub-intervals $[l, m]$ and $[m + 1, r]$. In a generalized segment tree, $m$ is not required to be exactly the midpoint of the interval, but it still must satisfy $l \le m < r$. It is not hard to see that in a generalized segment tree, the depth of the tree can reach $O(n)$. 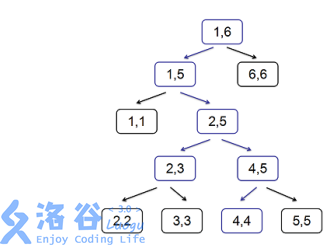For example, the following tree is a generalized segment tree:  For convenience, we number all nodes of the segment tree by preorder traversal. For example, in the figure above, the number of $[2, 3]$ is $5$, and the number of $[4, 4]$ is $9$. It is not hard to see that a generalized segment tree built on $[1, n]$ has a total of $2n - 1$ nodes. Consider transplanting the interval-location operation on a segment tree (this is what is done when applying lazy tags) to a generalized segment tree. You can find that on a generalized segment tree, you can still locate an interval using the traditional segment tree method. For example, in the figure above, the blue nodes and blue edges are the nodes and edges passed when locating interval $[2, 4]$, and the final located nodes are $[2, 3]$ and $[4, 4]$. If you are not familiar with segment trees, here is a formal definition of the interval-location operation. Given an interval $[l, r]$, find as few segment tree nodes as possible whose intervals are **pairwise disjoint**, such that the union of their intervals is **exactly** $[l, r]$. Define $S_{[l,r]}$ as the set of nodes obtained by locating interval $[l, r]$. For example, in the figure above, $S_{[2,4]} = \{5, 9\}$. Define the distance $d(u, v)$ between two nodes $u, v$ on the segment tree as the number of edges on the shortest path from $u$ to $v$ on the segment tree. For example, in the figure above, $d(5, 9) = 3$. Now, Ke Lian gives you a generalized segment tree on $[1, n]$ and $m$ queries. Each query gives three integers $u, l, r\ (l \le r)$. Ke Lian wants to know $\sum_{v \in S_{[l, r]}} d(u, v)$.

The first line contains an integer $n$. The next line contains $n - 1$ space-separated integers. In increasing order of node number, they give the split position $m$ of every **non-leaf** node in the generalized segment tree. It is not hard to see that this information uniquely determines a generalized segment tree on $[1, n]$. The next line contains an integer $m$. Then follow $m$ lines. Each line contains three integers $u, l, r\ (1 \le u \le 2n - 1, 1 \le l \le r \le n)$, representing a query.

For each query, output one integer as the answer.

| Test Point ID | $n$ | $m$ | Other Constraints | | :------: | :-----------------: | :-----------------: | :---: | | $1$ | $\le 100$ | $\le 100$ | None | | $2$ | $\le 2 \times 10^5$ | $\le 20$ | None | | $3,4$ | $\le 2 \times 10^5$ | $\le 2 \times 10^5$ | $r = n$ | | $5,6$ | $\le 2 \times 10^5$ | $\le 2 \times 10^5$ | $u = 1$ | | $7,8,9,10$ | $\le 2 \times 10^5$ | $\le 2 \times 10^5$ | None | For $100\%$ of the testdata, it is guaranteed that $n \ge 2, m \ge 1$. Translated by ChatGPT 5