P5232 [JSOI2012] The Wise One’s Trial

In the year $1371$ AD, the Founding Emperor ordered the construction of large temples on Beijige. In just a few years, ten temples were built on Jilong Mountain: the Imperial Temple, Guan Gong Temple, Zhenwu Temple, Merit Officials Temple, Jiang Wang Temple, Capital City God Temple, Bian Hu Temple, Martyrs Temple, King Liu Yue Temple, and King Cao Wuhui Temple. Together, they were called the “Ten Temples”. Later, to make it easier for people to come to Jilong Mountain to burn incense and worship, the emperor ordered the clearing of the long-silted tidal ditch at the foot of Jilong Mountain. Thus, the “Incense River” came into being. However, not everyone was allowed to go to Jilong Mountain. The emperor built a stone bridge over the Incense River, and in the middle hung a mechanism grid of height $Rx$ and width $Ry$ (as shown in the figure below). All cells can be flipped; one side is white and the other side is black. Here we use $0$ to represent white and $1$ to represent black. Initially, all cells show the white side. There are $Rx+Ry$ mechanism buttons corresponding to the $Rx$ rows and the $Ry$ columns. Once a button is triggered, the cells in the corresponding row or column are flipped simultaneously.  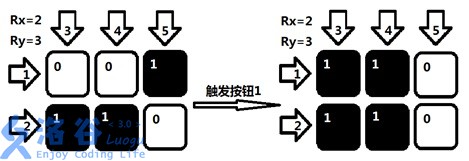Meanwhile, the strategist Liu Ji, who was good at observing celestial phenomena, provided a black-and-white pattern called the “Misfortune Star”. Each person passing by and heading to Jilong Mountain must trigger exactly one button. After triggering, if the resulting pattern matches the “Misfortune Star”, the visitor is not allowed to pass. The number of people coming to Jilong Mountain each day is known in advance and is $N$. Also, since the empire’s power is overwhelming, each visitor at the beginning always has a high probability of triggering button number $1$. We use a sequence $A_1, A_2, \dots, A_N$ to represent this, and it is guaranteed that initially all elements of $A$ are $1$. Throughout the problem, $A_i$ satisfies $1 \leq A_i \leq Rx+Ry$. The emperor cares a lot about how many people are not allowed to go to Jilong Mountain. So from time to time, he asks: “During a certain period of time, how many people cannot pass the ‘Misfortune Star’ trial?”. However, the scholars and poets coming to Jilong Mountain do not want such a single kind of operation. A visitor may suddenly decide to change the button they will trigger. In an even more troublesome case, several consecutive people traveling together may suddenly decide to change their buttons and all trigger the same button. Now this troublesome problem is handed over to you.

The first line contains two integers $Rx$ and $Ry$, representing the height and width of the mechanism grid (as shown in the figure). Then follow $Rx$ lines, each containing $Ry$ digits, describing the “Misfortune Star” pattern. Each digit is either $0$ or $1$. The next line contains two integers $N$ and $M$, representing the number of people and the number of queries/modifications. Then follow $M$ lines, each corresponding to one query or modification. Each line starts with an integer $t$: If $t$ is $0$: then two integers $d$ and $x$ follow, meaning set $A_d$ to $x$. If $t$ is $1$: then two integers $l$ and $r$ follow, meaning query how many people from the $l$-th to the $r$-th person will produce the “Misfortune Star” pattern after triggering their button, and thus cannot pass. If $t$ is $2$: then three integers $l$, $r$, and $x$ follow, meaning set $A_l, A_{l+1}, \dots, A_{r-1}, A_r$ all to $x$.

For each query (i.e., the case $t$ is $1$), output a single line containing one integer, describing the number of people in the interval $[l, r]$ that meet the requirement.

For $40\%$ of the testdata, $N \leq 5000$, $M \leq 10000$. For $70\%$ of the testdata, $N \leq 130000$, $M \leq 30000$. For $100\%$ of the testdata, $N \leq 1000000$, $M \leq 120000$, $Rx \leq 2$, $Ry \leq 3$. Translated by ChatGPT 5