P5235 [WC2017] Chessboard.

Xiao Z is playing a game on a chessboard. This chessboard is an undirected connected graph with $n$ vertices and $m$ edges. The vertices are labeled with positive integers in $[1,n]$. At the beginning of the game, each vertex has one piece placed on it. Each piece has an integer in $[0,n-1]$, representing the piece’s label. All piece labels are distinct. In each operation, Xiao Z must first choose an edge of the graph such that one endpoint of this edge currently has the piece labeled $0$. Then, Xiao Z swaps the pieces on the two endpoints of this edge. Now you are given the graph (the chessboard) and the initial label of the piece on each vertex. Xiao Z asks you to answer $q$ queries. Each query specifies a target state of the chessboard. You need to determine whether it is possible, using some number of operations, to transform the chessboard from the initial state into the target state.

The first line contains three positive integers $n,m,q$, representing the number of vertices, the number of edges, and the number of queries. The next $m$ lines each contain two integers $u,v(1\leq u,v\leq n)$, indicating an undirected edge connecting vertices $u$ and $v$. It is guaranteed that $u\neq v$, so there are no self-loops. It is guaranteed that the given graph is connected, i.e., any two vertices can reach each other through some edges. The next line contains $n$ space-separated integers. The $i$-th integer denotes the label of the piece on vertex $i$ in the initial state. It is guaranteed that all labels are integers in $[0,n-1]$ and are pairwise distinct. The next $q$ lines each contain $n$ space-separated integers describing one query. The $i$-th integer denotes the label of the piece on vertex $i$ in the target state. It is guaranteed that all labels are integers in $[0,n-1]$ and are pairwise distinct.

Output $q$ lines. Each line contains a string ```Yes``` or ```No```. ```Yes``` means the target state in the query can be reached from the initial state using some number of operations, and ```No``` means it is impossible. Note that the first letter of both ```Yes``` and ```No``` is uppercase.

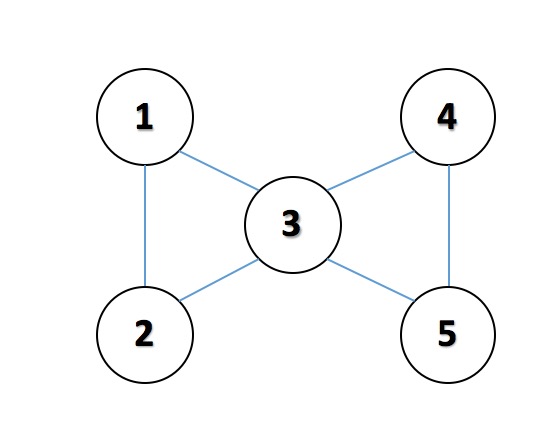
The samples are shown in the figure:  For the first query, it is enough to move the piece labeled $0$ along the path $5-4-3-2-1$. For the second query, move the piece labeled $0$ along $5-3-1-2-3$. The third query has no solution. All testdata satisfy: $1 \leq n \leq 50$, $1 \leq m \leq 100$, $1 \leq q \leq 1000$. | Test Point ID | $n$ | $m$ | Data Property | | :-----: | :---------: | :-----------: | :----: | | 1 | $\leq 8$ | $\leq 15$ | None | | 2 | $\leq 8$ | $ = n-1 $ | None | | 3 | $\leq 50$ | $ = n-1 $ | None | | 4 | $\leq 50$ | $ =n $ | None | | 5 | $\leq 50$ | $ =n $ | Property 1 | | 6 | $\leq 50$ | $ =n $ | Property 1 | | 7 | $\leq 50$ | $ =n $ | None | | 8 | $\leq 50$ | $ =n $ | None | | 9 | $\leq 50$ | $ \leq 100$ | Property 2 | | 10 | $\leq 50$ | $ \leq 100$ | Property 2 | | 11 | $\leq 50$ | $ \leq 100$ | Property 3 | | 12 | $\leq 50$ | $ \leq 100$ | Property 3 | | 13 | $\leq 50$ | $ \leq 100$ | Property 3 | | 14 | $\leq 50$ | $ \leq 100$ | None | | 15 | $\leq 50$ | $ \leq 100$ | None | | 16 | $\leq 50$ | $ \leq 100$ | None | | 17 | $\leq 50$ | $ \leq 100$ | None | | 18 | $\leq 50$ | $ \leq 100$ | None | | 19 | $\leq 50$ | $ \leq 100$ | None | | 20 | $\leq 50$ | $ \leq 100$ | None | - Property 1: The degree of every vertex is $2$. - Property 2: This chessboard can be drawn on a $k \times k$ rectangular grid graph, where $k \times k=n$ and $2k \times (k-1)=m$. - Property 3: Each edge belongs to at most one simple cycle. Translated by ChatGPT 5