P5251 [LnOI2019] 第二代图灵机

1989年，Abbi提出了一种抽象的计算模型 —— 第二代图灵机 (The 2nd Generation Turing Machine）。 所谓的第二代图灵机就是指一个抽象的机器，它有一条长度为$n$的纸带，纸带分成了$n$个小方格，每个方格有不同的**颜色**和不同的**数字**。 

第二代图灵的基本思想是用机器来模拟鹿们用纸笔进行数学运算的过程，他把这样的过程看作下列两种简单的动作： 1. 在纸带上的一格写数字。 2. 在纸带上的一段区间着色。 为了测试第二代图灵机的性能，Abbi提出了一种用于判定机器是否具有智能的试验方法，即图灵试验。 1. 求 $[l,r]$ 中包含所有(一共 $c$ 种)颜色，数字和最小的子区间的数字和。 2. 求 $[l,r]$ 中没有重复颜色，数字和最大的子区间的数字和。 你需要为第二代图灵机编写算法，使他能通过所有的图灵试验。为保证试验的正确性，所有数据都是随机生成的。

第一行输入两个正整数 $n,m,c$，分别表示纸带长度，操作次数和颜色总数。 第二行 $n$ 个非负整数，表示每个格子上的初始数字 $a_i$。 第三行 $n$ 个非负整数，表示每个格子上的颜色编号 $b_i$。 接下来 $m$ 行，对应每一次操作。 操作一格式：$1\quad x\quad y$，表示将第 $x$ 位的数字改为 $y$，保证 $1≤y≤10000$。 操作二格式：$2\quad l\quad r\quad y$，表示将区间 $[l,r]$ 的颜色全部改为 $y$ ，保证 $1≤y≤c$。 操作三格式：$3\quad l\quad r$，表示询问区间$[l,r]$中包含所有(一共$c$种)颜色，数字和最小的子区间的数字和。 操作四格式：$4\quad l\quad r$，表示询问区间$[l,r]$中没有重复颜色，数字和最大的子区间的数字和。

对于操作三和操作四，输出一个整数，表示最小或最大的数字和。 对于操作三，若不存在满足条件的子区间，请输出 $-1$。

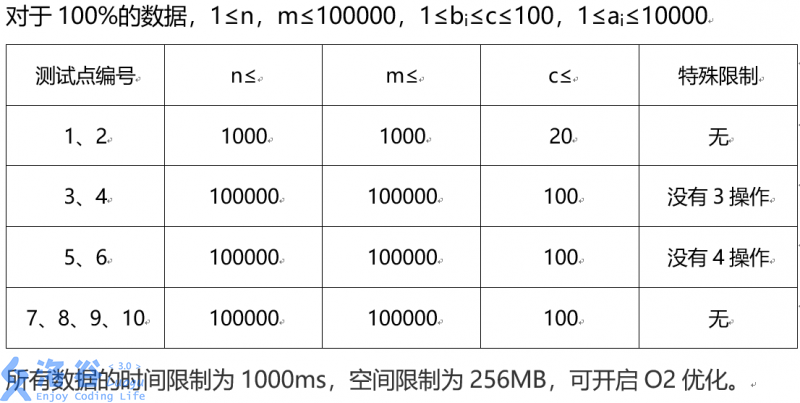
 **由于数据规模较大，建议用以下方法读入一个正整数。** ```cpp void read(int &x){ char ch; while(ch = getchar(), ch < '!'); x = ch - 48; while(ch = getchar(), ch > '!') x = (x