P5251 [LnOI2019] The 2nd Generation Turing Machine

In 1989, Abbi proposed an abstract computation model — the 2nd Generation Turing Machine (The 2nd Generation Turing Machine). The so-called 2nd Generation Turing Machine refers to an abstract machine that has a tape of length $n$. The tape is divided into $n$ small cells. Each cell has a different **color** and a different **number**. 

The basic idea of the 2nd Generation Turing Machine is to use a machine to simulate the process of deer doing mathematical calculations with pen and paper. He regarded such a process as the following two simple actions: 1. Write a number in one cell on the tape. 2. Color a segment of the tape. To test the performance of the 2nd Generation Turing Machine, Abbi proposed a method to determine whether the machine is intelligent, namely the Turing test. 1. For $[l,r]$, query the sum of numbers of the subsegment with the minimum sum that contains all (a total of $c$ types of) colors. 2. For $[l,r]$, query the sum of numbers of the subsegment with the maximum sum that has no repeated colors. You need to write an algorithm for the 2nd Generation Turing Machine so that it can pass all Turing tests. To ensure the correctness of the tests, all testdata are randomly generated.

The first line contains three positive integers $n,m,c$, representing the tape length, the number of operations, and the total number of colors. The second line contains $n$ non-negative integers, representing the initial number $a_i$ in each cell. The third line contains $n$ non-negative integers, representing the color ID $b_i$ of each cell. The next $m$ lines describe the operations. Operation 1: $1\quad x\quad y$, meaning to change the number at position $x$ to $y$, with $1≤y≤10000$ guaranteed. Operation 2: $2\quad l\quad r\quad y$, meaning to change the colors of all cells in the interval $[l,r]$ to $y$, with $1≤y≤c$ guaranteed. Operation 3: $3\quad l\quad r$, meaning to query, within $[l,r]$, the sum of numbers of the subsegment with the minimum sum that contains all (a total of $c$ types of) colors. Operation 4: $4\quad l\quad r$, meaning to query, within $[l,r]$, the sum of numbers of the subsegment with the maximum sum that has no repeated colors.

For Operation 3 and Operation 4, output one integer, representing the minimum or maximum sum of numbers. For Operation 3, if there is no subsegment that satisfies the condition, output $-1$.

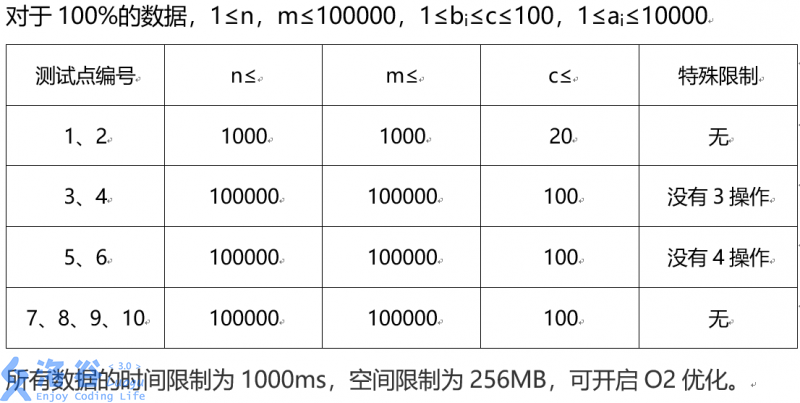
 **Since the data size is large, it is recommended to read a positive integer using the following method.** ```cpp void read(int &x){ char ch; while(ch = getchar(), ch < '!'); x = ch - 48; while(ch = getchar(), ch > '!') x = (x