P5254 [JSOI2013] Advertising Plan

Nowadays, painting some advertisements on the walls of buildings or on the surface of fence posts is a new way to attract attention.

Now, a small company run by Little G decided to try this kind of advertising as well. Little G freed up some space on his fence posts for advertisements. Each fence post is a horizontal $1*1*L$ quadrangular prism, and one $1*L$ face can be used for advertising. The $1*L$ face is divided into $L$ $1*1$ small squares (more specifically, $L$ consecutive squares arranged horizontally), and each square contains one letter. Over time, with more and more ads, troublesome situations may occur, such as plan changes or production mistakes. As a result, Little G’s warehouse has accumulated many useless fence posts that already have $L$ letters written on them. (All fence posts have the same size; the only difference is what letters are written on them.) Little G decided to reuse these fence posts and came up with some new ideas. 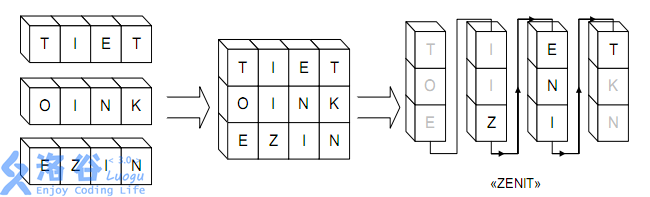If we stack these fence posts vertically, and then from left to right, for each fence post read the letters on it from top to bottom, we can obtain some new longer words, as shown in the picture:  These new words can meet some new needs of Little G. Of course, for aesthetic reasons, Little G does not allow you to delete or modify the letters that are already written on the fence posts. We describe this process more precisely. We stack $K$ fence posts of length $L$ together, obtaining a face with $K$ rows and $L$ columns, containing a total of $K*L$ letters, where each letter lies in its own unique cell. Starting from the top-left corner and reading each letter downward in order, we get a sequence of letters. For example, in the figure above, the result is “TOEIIZENITKN”. If this string contains the word we need, then obviously we only need to paint some cells white to obtain the desired word. For instance, if Little G wants to make an ad for Zenit, the football team of Saint Petersburg, then clearly the method in the picture can achieve what Little G wants. Now Little G has decided what advertisement to make, and he also provides you with the descriptions of the types of fence posts in his warehouse. You may assume that there are infinitely many fence posts of each type. Little G now wants to know the minimum number of fence posts that must be stacked to produce the advertisement Little G wants.

The first line contains two natural numbers, $N$ and $L$. The next $N$ lines each contain $L$ lowercase letters, describing the letters written on one type of fence post. It is guaranteed that the letter sequences on different types of fence posts are all different, and there are infinitely many fence posts of each type. The last line is a string $s$, representing the advertising slogan Little G has decided on.

The first line contains an integer $K$, indicating the minimum number of fence posts needed (note that this is the quantity, not the number of types).

$1~\leq~N,~L~\leq~100$ $1~\leq~|s|~\leq~200$ Translated by ChatGPT 5