P5260 [JSOI2013] Hypercube.

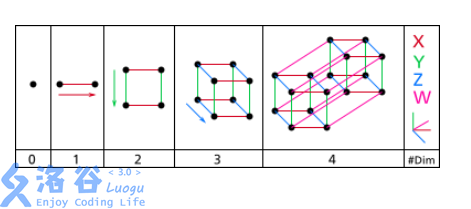
A hypercube is an extension of a cube into higher-dimensional space (it becomes a square in 2D and a line segment in 1D). In theoretical computer science, a hypercube is often related to binary encoding. Will, who has done quite a bit of research in theoretical computer science, naturally has his own thoughts about hypercubes.  The figure above shows the shapes corresponding to hypercubes in $0$ to $4$ dimensions. Clearly, we can view each vertex of a hypercube as a point, and each edge as a graph edge. In this way, we get an undirected graph, which we call a hypercube graph.

A $D$-dimensional hypercube graph has $2^D$ vertices. We label these vertices from $0$ to $2^D - 1$. There is an interesting and important necessary and sufficient conclusion: there must exist a way of labeling such that, for any two adjacent vertices in the graph, their labels’ binary codes differ in exactly one bit. In 2D and 3D, this can be understood intuitively as follows. For 2D, we can place the square in the first quadrant so that its four vertices, in counterclockwise order, are $(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$. Then treat each coordinate as a 2-bit binary number, and label these four points as $0, 1, 3, 2$. For 3D, similarly, we can make one vertex of the cube coincide with the origin, and make all edges parallel to the coordinate axes. Then determine the coordinates of the 8 points, and finally treat each 3D coordinate as a 3-bit binary number. For $D$ dimensions, do the same, and so on. Now, given an undirected graph with $N$ vertices and $M$ edges (vertices are labeled from $0$ to $N - 1$), Will wants to know whether this graph is isomorphic to a hypercube graph.

The first line contains an integer $Q$, meaning there are $Q$ queries in this input. Then follow $Q$ queries. For each query, the input format is: The first line contains two integers $N$ and $M$. The next $M$ lines each contain two different integers $x, y$, indicating that there is an undirected edge between vertex $x$ and vertex $y$ in the graph ($0 \le x, y < N$).

1. If the graph given in a query is not isomorphic to any hypercube graph, output $-1$. 2. If it is isomorphic to some hypercube graph, please relabel these $N$ vertices, and output on this line $N$ integers separated by spaces. The $i$-th integer denotes the new label of vertex $i$ in the original graph, such that after relabeling, the conclusion described in the statement is satisfied. Note: Each line of the output file must either contain only one integer $-1$, or contain a permutation of $N$ numbers from $0$ to $N - 1$. If there are multiple solutions, output any one.

$Q \leq 3, N \leq 32768, M \leq 1000000$. Translated by ChatGPT 5