P5270 无论怎样神树大人都会删库跑路

众所周知，神 J（Joker）每隔几天就会去成都法中假装上课，实际上是去玩指针。神J可以趁别人不注意掏出指针把自己指到任何位置（生物标本柜里大变活人？），或者把两个人的指针交换一下（成都法中版《你的名字》？），或者对着 OJ 念系统命令使得 OJ 随机变慢（mcfx：怎么这 CPU 睿频后反而变慢了）。 神树大人很不满意，因为树必须站在原地，而且神树大人也不会指针。但是神树大人是神，于是他打算把这个宇宙的数据库删了跑路，这样无所事事的神 J 就只能和神树大人玩牌了。

现在有个长为 $T$ 的字符串 $S$ 和 $n$ 个小字符串 $a_i$。 给定一个长为 $m$ 的数组 $R$，数组下标从 1 开始，初始有一个空字符串 $X$，神树大人打算进行 $Q$ 次操作，第 $i$ 次操作会把小字符串 $a_{R_{(i-1)\bmod m+1}}$ 丢到这个 $X$ 的末尾。 每次操作后，神树大人会检查这个字符串 $X$ 是否存在一个后缀使得任意排列后可以变成 $S$。 问有多少次这个字符串 $X$ 存在一个后缀使得**任意排列**后可以变成 $S$（即所有字符出现次数相同）。 可惜的是，这个字符串字符大小高达 $10^5$，所以你必须读入一个整数数组

输入 $n,T,Q$。 接下来输入 $T$ 个数表示字符串 $S$。 接下来输入 $n$ 行，每行第一个数 $len$ 表示长度，接下来输入 $len$ 个数表示这个小字符串，输入的每个数都在 $[0,10^5]$ 范围内。 接下来输入 $m$。 输入一行 $m$ 个数，表示 $R$。

输出答案。

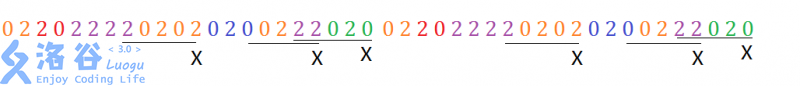
### 样例 1 解释  ### 数据范围 对于所有数据，$n,T,m\leq 10^5,1\leq R_i\leq n,Q\leq 10^9$，所有小字符串的总长不超过 $10^5$，所有字符 $\in[0,10^5]$。 | 子任务 | $n$ | $T$ | $Q$ | $m$ | 特殊性质 | | :-: | :-: | :-: | :-: | :-: | :- | | 1(20分) | $n \le 10$ | $T \le 10$ | $Q \le 100$ | $m \le 10$| 字符集为 $[0,5]$，小字符串总长不超过 $100$ | | 2(30分) | $n \le 10^3$ | $T \le 100$ | $Q \le 10^9$ | $m \le 10^3$| 字符集为 $[0,5]$，$R_i=i,n=m$，小字符串总长不超过 $100000$ | | 3(10分) | $n \le 10^5$ | $T \le 10^5$ | $Q \le 10^9$ | $m \le 10^5$| 字符集为 $[0,5]$，$R_i=i,n=m$ | | 4(40分) | $n \le 10^5$ | $T \le 10^5$ | $Q \le 10^9$ | $m \le 10^5$||