P5272 Anyway, God J Is Going to Practice Basketball.

God J and Lord God Tree are developing a sleep program. After running it, people can randomly see a corner of the universe in their dreams. Of course, most of the time that corner is dark, so people always feel that they did not dream at all. God J left a backdoor: as long as he controls a pointer, he can “assign” someone’s dream. So God J controls Lord God Tree’s dreams every day to write code. Lord God Tree is very unhappy, because a tree has to sleep every day. Lord God Tree is a god, and he already knew that God J was controlling things behind the scenes, so he also left a backdoor: as long as you enter a special command, you can force God J to sleep and do anything in the dream. One day, God J suddenly found himself in a huge basketball court, with many trainees practicing a 3-on-3 basketball game. “Why are you standing there like an idiot?” Lord God Tree walked over blowing a whistle. “Go practice. The KFC 3-on-3 National Finals are coming. Go score 114514 shots, then dribble past 1919810 people. zcy, come over and watch him.” A basketball suddenly appeared in God J’s hand. So God J practiced basketball for an entire afternoon under zcy’s supervision.

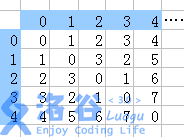
To prevent God J from using a basketball to create a pointer and point himself out, Lord God Tree forces God J to use basketballs to build a matrix. This matrix is infinite. Rows and columns are indexed starting from 0, and $a[i][j]=i\ xor\ j$.  Now, for a submatrix with top-left corner $(lx,ly)$ and bottom-right corner $(rx,ry)$, we randomly select a $W\times H$ matrix from it $K$ times $(K\leq 10^9)$. Ask for the probability that all selected matrices are exactly the same, modulo $10^9+7$.

The first line contains an integer $Q$, meaning there are $Q$ queries. Then $Q$ lines follow, each containing 7 integers $lx,rx,ly,ry,W,H,K$.

Output the answer modulo $10^9+7$. It is guaranteed that the answer exists.

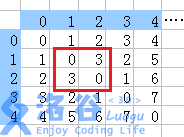
For the query `1 2 1 2 1 1 2`:  The matrices that can be selected are: 0 and 3, each appearing twice. There are the following cases: First pick 3, second pick 0, a total of 4 ways. First pick 3, second pick 3, a total of 4 ways. First pick 0, second pick 0, a total of 4 ways. First pick 0, second pick 3, a total of 4 ways. There are 16 ways in total, and the valid ones are $4+4=8$ ways. So the answer is $8/16=500000004(mod\ 10^9+7)$. ## Constraints For all testdata, $0\leq lx\leq rx\leq 10^9,0\leq ly\leq ry\leq 10^9,W\leq rx-lx+1,H\leq ry-ly+1,1\leq K\leq 10^9,Q\leq 10^3$.  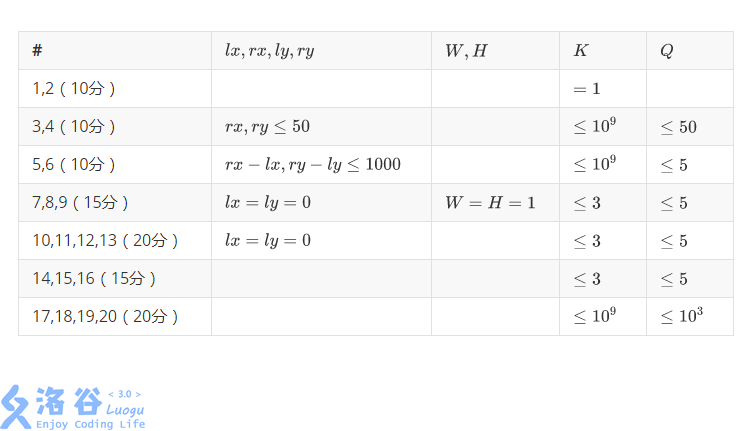Blank means there are no special constraints. Translated by ChatGPT 5