P5280 [ZJOI2019] Segment Tree

Jiutiao Kelian is a girl who likes data structures. Among common data structures, her favorite is the segment tree. The core of a segment tree is lazy propagation. Below is pseudocode for a segment tree with lazy tags, where the array $tag$ is the lazy tag:  Here, the function $\operatorname{Lson}(Node)$ denotes the left child of $Node$, and $\operatorname{Rson}(Node)$ denotes the right child of $Node$. Now Kelian has a segment tree over $[1,n]$, with index $1$. All nodes in this segment tree have $tag = 0$. Then Kelian performs $m$ operations. There are two types of operations: - $1\ l\ r$: Suppose Kelian currently has $t$ segment trees. She will copy each segment tree into two copies (the $tag$ array is copied as well). The segment tree originally indexed $i$ becomes two copied trees indexed $2i-1$ and $2i$. After copying, she has $2t$ segment trees in total. Then, she performs $\operatorname{Modify}(root,1,n,l,r)$ once on every segment tree whose index is odd. - $2$: Kelian defines the weight of a segment tree as the number of nodes in it whose $tag$ equals $1$. She wants to know the sum of weights of all segment trees she currently has.

The first line contains two integers $n,m$, denoting the initial interval length and the number of operations. Each of the next $m$ lines describes one operation. The input guarantees $1 \le l \le r \le n$.

For each query, output one integer per line representing the answer. The answer can be very large, so output it modulo $998244353$.

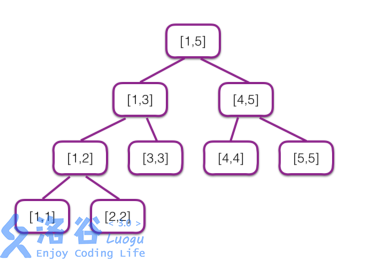
The segment tree over $[1,5]$ is shown below:  At the first query, Kelian has one segment tree, and there are no marks on any node, so the answer is $0$. At the second query, Kelian has two segment trees. By their indices, their marked nodes are: 1. Node $[1,3]$ is marked, so the weight is $1$. 2. No node is marked, so the weight is $0$. So the answer is $1$. At the third query, Kelian has four segment trees. By their indices, their marked nodes are: 1. Nodes $[1,2],[3,3],[4,5]$ are marked, so the weight is $3$. 2. Node $[1,3]$ is marked, so the weight is $1$. 3. Nodes $[3,3],[4,5]$ are marked, so the weight is $2$. 4. No node is marked, so the weight is $0$. So the answer is $6$. |Test Point|$n$|$m$|Other Constraints| |:-:|:-:|:-:|:-:| |$1$|$\le 1000$|$\le 10$|None| |$2$|^|^|^| |$3$|^|$\le 1000$|^| |$4$|^|^|^| |$5$|$\le 10^5$|$\le 10^5$|There is only one query| |$6$|^|^|^| |$7$|^|^|^| |$8$|^|^|None| |$9$|^|^|^| |$10$|^|^|^| For $100\%$ of the data, $1 \le l \le r \le n$. Translated by ChatGPT 5