P5286 [HNOI2019] Fish

$\text{\color{white}It is said that the testdata for this problem has no issues?}$

On the plane coordinate system, you are given $n$ distinct lattice points (that is, points whose $x$- and $y$-coordinates are both integers). We call an ordered 6-tuple $(A,B,C,D,E,F)$ formed by choosing 6 different points among these $n$ points a “fish” if and only if: $AB=AC$, $BD=CD$, and $DE=DF$ (the body must be symmetric), and both $\angle BAD,\angle BDA$ and $\angle CAD,\angle CDA$ are acute angles (the head and the tail obviously cannot be concave), and $\angle ADE,\angle ADF$ are greater than $90^\circ$ (that is, obtuse angles or straight angles, so that the tail will not stick up awkwardly). 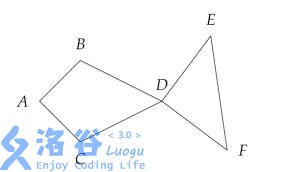The figure below shows an example of a valid fish:  Fish that consist of the same set of points but in different orders are considered different fish. For example, $(A,B,C,D,E,F)$ and $(A,C,B,D,E,F)$ are considered two different fish (after all, a fish has a back and a belly). Similarly, $(A,B,C,D,E,F)$ and $(A,B,C,D,F,E)$ are also considered two different fish (suppose the fish tail can be tied into a knot). Given the $n$ points, find how many fish can be formed. In particular, the input guarantees that all $n$ points are pairwise distinct.

The first line contains a positive integer $n$, representing the number of points on the plane. The next $n$ lines each contain two integers $x,y$, representing the coordinates of a point.

Output one line with a non-negative integer, representing the number of fish.

For the first 20% of the data, it is guaranteed that $n \leq 10,|x|,|y| \leq 5$. For the first 40% of the data, it is guaranteed that $n \leq 300$, $0 \leq |x|,|y| \leq 10^5$. For another 20% of the data, it is guaranteed that $|x|,|y| \leq 20$. For all data, it is guaranteed that $6 \leq n \leq 1000$, $0 \leq |x|, |y| \leq 10^9$, and the $n$ points are pairwise distinct. Translated by ChatGPT 5