P5288 [HNOI2019] 多边形

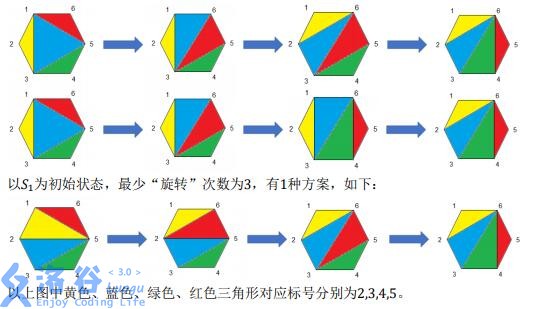
小 R 与小 W 在玩游戏。 他们有一个边数为 $n$ 的凸多边形，其顶点沿逆时针方向标号依次为 $1,2,3,\cdots , n$。最开始凸多边形中有 $n$ 条线段，即多边形的 $n$ 条边。这里我们用一个有序数对 $(a, b)$（其中 $a < b$）来表示一条端点分别为顶点 $a,b$ 的线段。 在游戏开始之前，小 W 会进行一些操作。每次操作时，他会选中多边形的两个互异顶点，给它们之间连一条线段，并且所连的线段不会与已存的线段重合、相交（只拥有一个公共端点不算作相交）。 他会不断重复这个过程，直到无法继续连线，这样得到了状态 $s_0$。$s_0$ 包含的线段为凸多边形的边与小 W 连上的线段，容易发现这些线段将多边形划分为一个个三角形区域。对于其中任意一个三角形，其三个顶点为 $i,j,k(i < j < k)$，我们可以给这个三角形一个标号 $j$，这样一来每个三角形都被标上了 $2,3, \cdots , n - 1$ 中的一个，且没有标号相同的两个三角形。 小 W 定义了一种“旋转”操作：对于当前状态，选定 $4$ 个顶点 $a,b,c,d$，使其满足 $1 \leq a < b < c

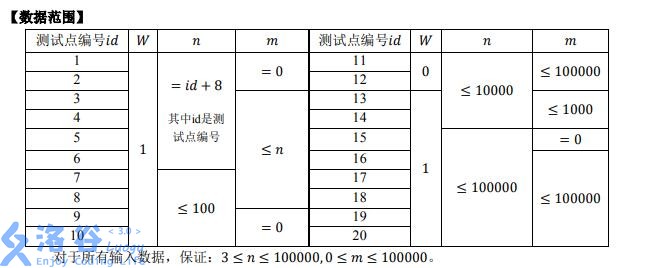
第一行一个整数 $W$，表示小 W 的心情。若 $W$ 为 $0$ 则只需求出最少的“旋转”次数，若 $W$ 为 $1$ 则还需求出“旋转”次数最少时的不同操作方案数。 第二行一个正整数 $n$，表示凸多边形的边数。 接下来 $n-3$ 行，每行两个正整数 $x,y$，表示小 W 在 $s_0$ 中连的一条线段，端点分别为 $x,y$。保证该线段不与已存的线段重合或相交。 接下来一行一个整数 $m$，表示小 W 以 $s_0$ 为基础产生的新状态个数。 接下来 $m$ 行，每行两个整数。假设其中第 $i$ 行为 $a,b$，表示对 $s_0$ 进行 $(a,b)$“旋转”后得到 $s_i$。

输出共 $m+1$ 行。 若 $W$ 为 $0$ 则每一行输出一个整数，第 $i(i = 1,2, \cdots , m, m + 1)$ 行输出的整数表示 $S_{i-1}$ 作为初始局面的最少“旋转”次数。 若 $W$ 为 $1$ 则每一行输出两个整数，第 $i(i = 1,2, \cdots , m, m + 1)$ 行输出的两个整数依次表示 $S_{i-1}$ 作为初始局面的最少“旋转”次数、“旋转”次数最少的不同操作方案数对 $10 ^ 9+7$ 取模的结果。