P5288 [HNOI2019] Polygon

Xiao R and Xiao W are playing a game. They have a convex polygon with $n$ sides, whose vertices are labeled $1,2,3,\cdots , n$ in counterclockwise order. Initially, there are $n$ line segments inside the convex polygon, namely the $n$ sides of the polygon. Here we use an ordered pair $(a, b)$ (where $a < b$) to represent a line segment whose endpoints are vertices $a,b$. Before the game starts, Xiao W performs some operations. In each operation, he chooses two distinct vertices of the polygon, draws a line segment between them, and the drawn segment will not overlap or intersect with any existing segment (having only one common endpoint is not considered an intersection). He repeats this process until no more segments can be added, obtaining a state $s_0$. The segments in $s_0$ include the polygon sides and the segments added by Xiao W. It is easy to see that these segments partition the polygon into triangular regions. For any such triangle with vertices $i,j,k(i < j < k)$, we can assign this triangle the label $j$. In this way, each triangle is labeled with a distinct number from $2,3, \cdots , n - 1$. Xiao W defines a kind of “rotation” operation: for the current state, choose $4$ vertices $a,b,c,d$ such that $1 \leq a < b < c

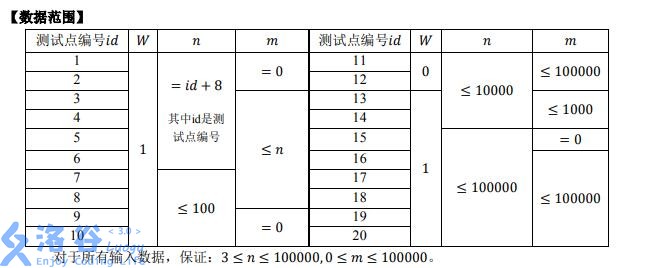
The first line contains an integer $W$, indicating Xiao W’s mood. If $W$ is $0$, you only need to output the minimum number of “rotations”. If $W$ is $1$, you also need to output the number of different operation plans when the number of “rotations” is minimal. The second line contains a positive integer $n$, the number of sides of the convex polygon. The next $n-3$ lines each contain two positive integers $x,y$, representing a segment drawn by Xiao W in $s_0$, with endpoints $x,y$. It is guaranteed that this segment does not overlap or intersect with existing segments. The next line contains an integer $m$, the number of new states generated by Xiao W based on $s_0$. The next $m$ lines each contain two integers. Suppose the $i$-th of these lines is $a,b$, meaning that $s_i$ is obtained by performing the $(a,b)$ “rotation” on $s_0$.

Output a total of $m+1$ lines. If $W$ is $0$, output one integer per line. On line $i(i = 1,2, \cdots , m, m + 1)$, the integer denotes the minimum number of “rotations” when $S_{i-1}$ is the initial state. If $W$ is $1$, output two integers per line. On line $i(i = 1,2, \cdots , m, m + 1)$, the two integers denote, respectively, the minimum number of “rotations” when $S_{i-1}$ is the initial state, and the number of different operation plans that achieve this minimum, modulo $10 ^ 9+7$.

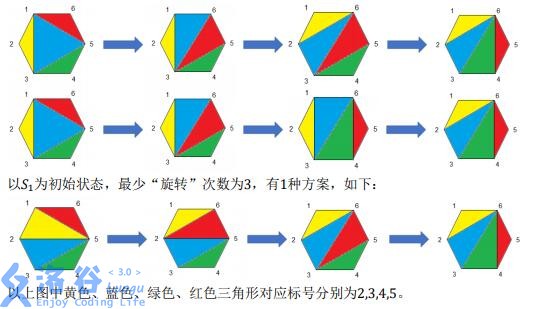
  Translated by ChatGPT 5