[GXOI/GZOI2019] 宝牌一大堆

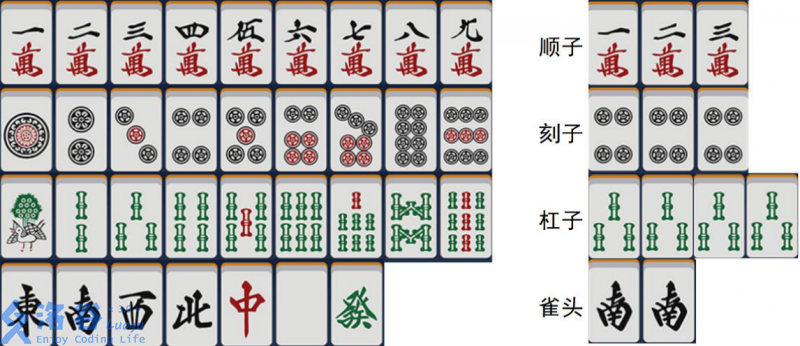
麻将是一种传统的博弈游戏，由 $4$ 名玩家参与，轮流摸牌、打牌。在竞技比赛中主要有国标麻将（中国）和立直麻将（日本）两大规则。本题采用一种特别的规则——「宝牌一大堆」规则。 #### 牌型 一副麻将由 $136$ 张牌组成，其中包含 $34$ 种不同的牌，每种各有 $4$ 张。这 $34$ 种牌分别是： 一万到九万、一索到九索、一筒到九筒、东、南、西、北、中、白、发。  它们可以组合成不同的牌型： - 顺子：$3$ 张数字连续的万，或 $3$ 张数字连续的索，或 $3$ 张数字连续的筒。 - 刻子：$3$ 张完全一样的牌。 - 杠子：$4$ 张完全一样的牌。 - 雀头：$2$ 张完全一样的牌。 其中顺子和刻子统称为面子。 #### 和牌 手牌（一名玩家持有的牌）宣告胜利的状况称为「和牌」。 - 当玩家持有 $14$ 张牌，并且满足以下三个条件之一时，判定为「和牌」： 1. 存在一种方案，使得这 $14$ 张牌可以分成 $4$ 组面子、$1$ 组雀头，简记为「$3 \times 4 + 2$」。 2. 存在一种方案，使得这 $14$ 张牌可以分成 $7$ 组**不同的**雀头，称为「七对子」。 3. 这 $14$ 张牌**仅由**一万、九万、一索、九索、一筒、九筒、东、南、西、北、中、白、发这 $13$ 种牌组成，并且这 $13$ 种牌**每种至少有 $1$ 张**，称为「国士无双」。 - 当玩家持有 $15$ 张牌，并且存在一种方案，使得这 $15$ 张牌可以分成 $1$ 组杠子、$3$ 组面子、$1$ 组雀头，判定为和牌。 - 当玩家持有 $16$ 张牌，并且存在一种方案，使得这 $16$ 张牌可以分成 $2$ 组杠子、$2$ 组面子、$1$ 组雀头，判定为和牌。 - 当玩家持有 $17$ 张牌，并且存在一种方案，使得这 $17$ 张牌可以分成 $3$ 组杠子、$1$ 组面子、$1$ 组雀头，判定为和牌。 - 当玩家持有 $18$ 张牌，并且存在一种方案，使得这 $18$ 张牌可以分成 $4$ 组杠子、$1$ 组雀头，判定为和牌。 #### 宝牌 每局游戏还会指定若干张「宝牌」，和牌时，手牌中的每张宝牌会使收益翻一番（会在接下来详细介绍）。 #### 达成分数 由于可以「和牌」的手牌很多，可以给每种判定为「和牌」的手牌定义一个「达成分数」，这个分数等于从所有尚未打出的牌中选出若干张，能够组成该手牌的方法数，再乘上手牌中 $2$ 的「宝牌数」次方。 该分数综合考虑了和牌几率与和牌收益，理论上以分数较高的手牌为目标较好。 例如下图手牌显然是可以「和牌」的，如果目前场上还剩 $3$ 张一万、$4$ 张九万，以及二到八万各 $2$ 张没有打出，宝牌为九万，那么下图手牌的「达成分数」就是 $C_3^3 C_4^3 C_2^2 (C_2^1)^6 2^3 = 2048$，其中 $C$ 表示组合数。  特别地，「七对子」和牌的手牌，达成分数额外乘 $7$。「国士无双」和牌的手牌，达成分数额外乘 $13$。 有一天，小 L，小 Y，小 I 和小 W 正在打麻将，路过的雪野和看到了所有已经打出的牌，但不知道任何一名玩家的手牌。也许你已经猜到了下面的剧情— —雪野和想知道在所有尚未打出的牌中，「达成分数」最高的可以「和牌」的手牌有多少分，但是她还要观看麻将比赛，所以这个问题就交给你了。

每个测试点包含多组数据，第一行是一个整数 $T$，表示数据组数。注意各组数据之间是互相独立的。 每组数据包含两行，第一行给出场上已经打出的牌，第二行给出该局的所有宝牌。 规定用 $\texttt{1m},\texttt{2m},\dots,\texttt{9m}$ 代表万，$\texttt{1p},\texttt{2p},\dots,\texttt{9p}$ 代表筒，$\texttt{1s},\texttt{2s},\dots,\texttt{9s}$ 代表索，$\texttt E,\texttt S,\texttt W,\texttt N$ 代表东、南、西、北，$\texttt Z,\texttt B,\texttt F$ 代表中、白、发，相邻两张牌之间用一个空格隔开，每行的末尾有一个单独的 $0$ 代表结束。

输出文件应包含 $T$ 行，对于每组数据，输出一个整数表示最高分数。

2
0
0
7m 4p 2s 7s 6p 8s 7p 5s 9s 9s 1p 5m 9m 5s 4p 5s E 1p 6s 5p B 4m 6m W 6p 6s E 9s 5p 2s 8s 8p 4m 3s 9m 5p 3s 2s 6s 8s 8p 6p 5m 4s 3m 4s 5s 4s 6m 9s 6p N 5m 7s 4m 2m 2s 6s 3m 7p B B N 1m 3m B 8p F 7p 0
W 4p N 3m 2m B 9m 3p 1p 6p S 4s 5p 8s 4m 5s 2s 3s 0

1308622848
127401984

### 样例解释 在第一组数据中，没有打出过任何牌，没有宝牌，和「国士无双」分数最高，为 $13 \times 6 \times 4^{12}$。 和「$3 \times 4 + 2$」和「七对子」的分数为 $100663296$ 和 $1959552$。 在第二组数据中，和「$3 \times 4 + 2$」分数最高，为 $127401984$，可以得到该分数的手牌之一为「$\texttt{1m2m3m 7m8m9m 1p2p3p 3p4p5p SS}$」。 和「七对子」的分数为 $125411328$，不存在和「国士无双」的可能。 ### 数据范围 保证已经打出的牌必定是合法的牌，且每种不超过 $4$ 张。宝牌不会重复给出。 |测试点编号|$T$ 的规模|已经打出的牌|宝牌数| |:-:|:-:|:-:|:-:| |$1$|$T = 10$|无特殊限制|$\le 20$ 张| |$2$|$T = 100$|至少包括所有数字为三到七的牌|$\le 20$ 张| |$3$|$T = 500$|每种至少 $2$ 张|$\le 20$ 张| |$4$|$T = 500$|每种至少 $3$ 张|$\le 20$ 张| |$5$|$T = 500$|无特殊限制|$0$ 张| |$6$|$T = 1,000$|无特殊限制|$0$ 张| |$7$|$T = 1,000$|无特殊限制|$\le 20$ 张| |$8$|$T = 1,500$|无特殊限制|$\le 20$ 张| |$9$|$T = 2,000$|无特殊限制|$\le 20$ 张| |$10$|$T = 2,500$|无特殊限制|$\le 20$ 张|