P5301 [GXOI/GZOI2019] A Pile of Dora Tiles

Mahjong is a traditional board game played by $4$ players, who take turns drawing and discarding tiles. In competitive matches, the two main rulesets are Chinese Official Mahjong (China) and Riichi Mahjong (Japan). This problem uses a special ruleset: “A Pile of Dora Tiles”. #### Tile Types A full mahjong set contains $136$ tiles, including $34$ different types of tiles, with $4$ copies of each type. These $34$ types are: $1$-man to $9$-man, $1$-sou to $9$-sou, $1$-pin to $9$-pin, East, South, West, North, Red, White, Green.  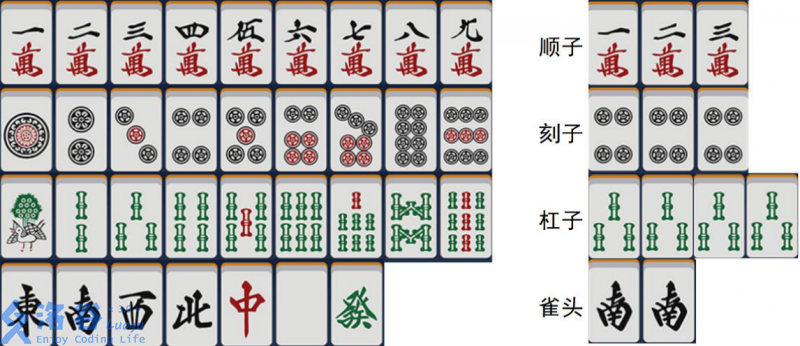They can form different groups: - Sequence: $3$ consecutive number tiles in manzu, or $3$ consecutive number tiles in souzu, or $3$ consecutive number tiles in pinzu. - Triplet: $3$ identical tiles. - Quad: $4$ identical tiles. - Pair: $2$ identical tiles. Sequences and triplets are collectively called melds. #### Winning Hand A hand (the tiles held by one player) that declares victory is called a “winning hand”. - When a player holds $14$ tiles and satisfies one of the following three conditions, it is a winning hand: 1. There exists a way to split these $14$ tiles into $4$ melds and $1$ pair, denoted as “$3 \times 4 + 2$”. 2. There exists a way to split these $14$ tiles into $7$ **distinct** pairs, called “Seven Pairs”. 3. These $14$ tiles consist **only of** the following $13$ tile types: $1$-man, $9$-man, $1$-sou, $9$-sou, $1$-pin, $9$-pin, East, South, West, North, Red, White, Green; and among these $13$ types, **each type appears at least once**. This is called “Thirteen Orphans”. - When a player holds $15$ tiles and there exists a way to split these $15$ tiles into $1$ quad, $3$ melds, and $1$ pair, it is a winning hand. - When a player holds $16$ tiles and there exists a way to split these $16$ tiles into $2$ quads, $2$ melds, and $1$ pair, it is a winning hand. - When a player holds $17$ tiles and there exists a way to split these $17$ tiles into $3$ quads, $1$ meld, and $1$ pair, it is a winning hand. - When a player holds $18$ tiles and there exists a way to split these $18$ tiles into $4$ quads and $1$ pair, it is a winning hand. #### Dora Tiles In each round, several “dora tiles” are also specified. When you win, each dora tile in your hand doubles the payoff (explained in detail below). #### Achieved Score Since there are many possible winning hands, we define an “achieved score” for each winning hand. This score equals: the number of ways to choose some tiles from all tiles that have not been discarded yet such that they form this hand, multiplied by $2^{(\text{number of dora tiles in the hand})}$. This score considers both the chance to win and the payoff after winning. In theory, it is better to aim for hands with higher scores. For example, the hand shown below is clearly a winning hand. If there are still $3$ copies of $1$-man, $4$ copies of $9$-man, and $2$ copies of each of $2$-man through $8$-man not yet discarded on the table, and the dora tile is $9$-man, then the achieved score of the hand below is $C_3^3 C_4^3 C_2^2 (C_2^1)^6 2^3 = 2048$, where $C$ denotes the binomial coefficient.  In particular, for a “Seven Pairs” winning hand, the achieved score is additionally multiplied by $7$. For a “Thirteen Orphans” winning hand, the achieved score is additionally multiplied by $13$. One day, Xiao L, Xiao Y, Xiao I, and Xiao W were playing mahjong. Yukino Wakana, who happened to pass by, saw all the tiles that had already been discarded, but did not know any player’s hand. Perhaps you have already guessed what happens next— —Yukino Wakana wants to know, among all tiles not yet discarded, what is the maximum achieved score of any winning hand. But she still needs to watch the mahjong match, so she leaves this problem to you.

Each test point contains multiple test cases. The first line is an integer $T$, the number of test cases. Note that the test cases are independent. Each test case consists of two lines. The first line gives the tiles already discarded on the table, and the second line gives all dora tiles for this round. We use $\texttt{1m},\texttt{2m},\dots,\texttt{9m}$ for manzu, $\texttt{1p},\texttt{2p},\dots,\texttt{9p}$ for pinzu, $\texttt{1s},\texttt{2s},\dots,\texttt{9s}$ for souzu, $\texttt E,\texttt S,\texttt W,\texttt N$ for East, South, West, North, and $\texttt Z,\texttt B,\texttt F$ for Red, White, Green. Adjacent tiles are separated by a single space, and each line ends with a standalone $0$ indicating the end.

The output should contain $T$ lines. For each test case, output one integer, the maximum score.

### Sample Explanation In the first test case, no tiles have been discarded, and there are no dora tiles. “Thirteen Orphans” has the highest score, which is $13 \times 6 \times 4^{12}$. The scores for “$3 \times 4 + 2$” and “Seven Pairs” are $100663296$ and $1959552$, respectively. In the second test case, “$3 \times 4 + 2$” has the highest score, which is $127401984$. One hand that achieves this score is “$\texttt{1m2m3m 7m8m9m 1p2p3p 3p4p5p SS}$”. The score for “Seven Pairs” is $125411328$, and it is impossible to form “Thirteen Orphans”. ### Constraints It is guaranteed that the discarded tiles are always legal tiles, and for each type there are no more than $4$ copies. Dora tiles are given without repetition. |Test Point ID|Scale of $T$|Discarded Tiles|Number of Dora Tiles| |:-:|:-:|:-:|:-:| |$1$|$T = 10$|No special restrictions|$\le 20$ tiles| |$2$|$T = 100$|Includes at least all number tiles from $3$ to $7$|$\le 20$ tiles| |$3$|$T = 500$|At least $2$ copies of each type|$\le 20$ tiles| |$4$|$T = 500$|At least $3$ copies of each type|$\le 20$ tiles| |$5$|$T = 500$|No special restrictions|$0$ tiles| |$6$|$T = 1,000$|No special restrictions|$0$ tiles| |$7$|$T = 1,000$|No special restrictions|$\le 20$ tiles| |$8$|$T = 1,500$|No special restrictions|$\le 20$ tiles| |$9$|$T = 2,000$|No special restrictions|$\le 20$ tiles| |$10$|$T = 2,500$|No special restrictions|$\le 20$ tiles| Translated by ChatGPT 5