P5302 [GXOI/GZOI2019] Aerobatic Flight

In the year $9012$, the aviation base of City Z plans to hold an aerobatic flight show. The show venue can be seen as a 2D Cartesian coordinate system, where the $x$-coordinate represents the horizontal position and the $y$-coordinate represents the flight altitude. In the initial plan, these $n$ aircraft will first fly to the starting line $x = x_{st}$. For aircraft $i$, its altitude at the start is $y_{i,0}$. Their destination is the ending line $x = x_{ed}$, where aircraft $i$ should be at altitude $y_{i,1}$. Therefore, each aircraft can be viewed as a point in the coordinate system, and its route is a line segment starting from $(x_{st}, y_{i,0})$ and ending at $(x_{ed}, y_{i,1})$, as shown below.  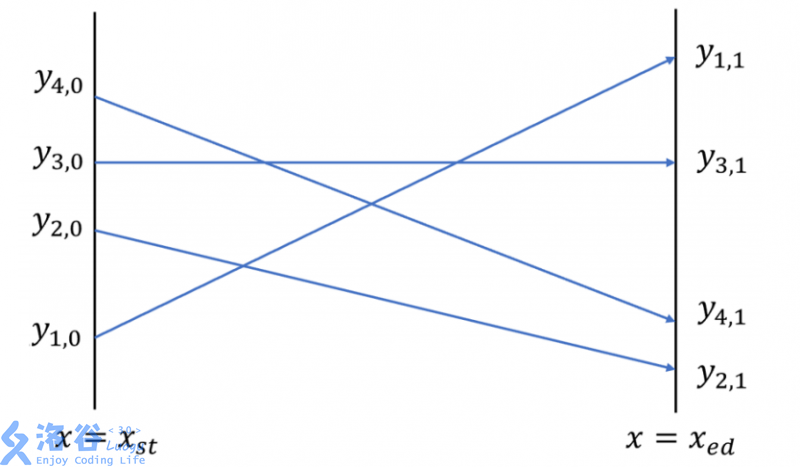All $n$ aircraft depart at the same time and always maintain a constant ground speed. Therefore, for any two intersecting routes (segments), the two corresponding aircraft will 반드시 reach the intersection point at the same time—this is the moment they perform an aerobatic stunt. They will bank their wings and perform a close “pass-by” stunt, and then **continue along their own routes**. 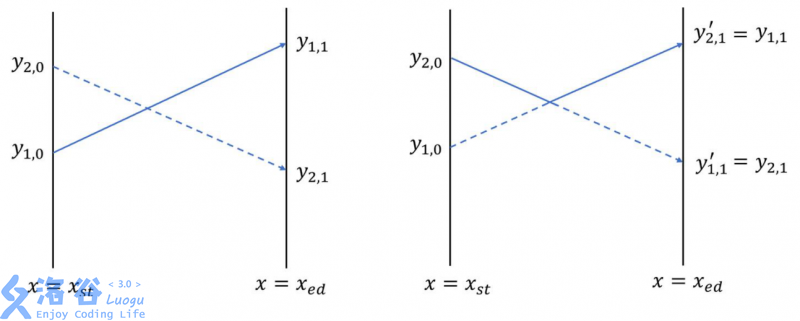The aviation base has also recently developed a new stunt called “head-on swap”. When two aircraft reach the intersection point, the one that was descending immediately starts climbing, while the one that was climbing performs a flip. The two aircraft pass the intersection point one above the other, belly to belly, also at a very close distance, and then **swap their remaining routes**. We do not need to care how these stunts are physically achieved. Aircraft are still treated as points. Under these two stunts, the route changes are shown below ($y_{i,1}'$ denotes the new ending altitude of aircraft $i$ after swapping routes). It is easy to see that “head-on swap” turns their routes into polylines and **keeps their relative order in the $y$-coordinate**; while “pass-by” **changes their relative order in the $y$-coordinate**.  Now, the visiting guests提出 a strict requirement: at the ending line $x = x_{ed}$, when sorting by altitude, the relative order of the $n$ aircraft must be the same as the relative order at $x = x_{st}$. The guests also assign difficulty coefficients $a$ and $b$ to the “head-on swap” stunt and the “pass-by” stunt, respectively. Each “head-on swap” gives a score of $a$, and each “pass-by” gives a score of $b$. In addition, there are $k$ guests. Guest $i$ stays in a hot-air balloon at position $(p_i, q_i)$ and has an observation range $r_i$, so they can observe all stunts within the region $|x - p_i| + |y - q_i| \le r_i$. If a stunt at some intersection point is observed by **one or more** guests, an extra bonus score of $c$ is obtained. 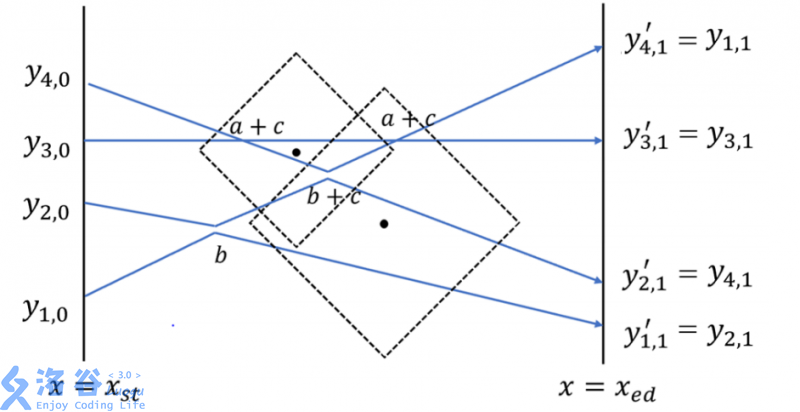Note: **Whether or not a stunt is observed, it still earns the score $a$ or $b$.** The figure below shows, for the $4$ routes and $4$ intersections in the first figure, one arrangement that meets the requirement: it includes $2$ “head-on swap” stunts, $2$ “pass-by” stunts, and $3$ stunts are observed, for a total score of $2a + 2b + 3c$. For easier viewing, the intersections where “head-on swap” occurs are drawn slightly separated.  In this story, you are the planner of City Z’s aviation base. You can decide, at each intersection point, whether to perform “head-on swap” or “pass-by”. You are required, while ensuring the guests’ requirement, to compute the minimum and maximum total scores that the whole aerobatic show can achieve.

The first line contains six non-negative integers $n, a, b, c, x_{st}, x_{ed}$, representing the total number of routes (segments), the score for the “head-on swap” stunt, the score for the “pass-by” stunt, the extra bonus for being observed, the $x$-coordinate of the starting line, and the $x$-coordinate of the ending line. The second line contains $n$ non-negative integers $y_{i,0}$. The $i$-th number is the $y$-coordinate of the start point of route $i$. It is guaranteed that they are given in increasing order, i.e. $y_{i,0} < y_{i + 1,0}$. The third line contains $n$ non-negative integers $y_{i,1}$. The $i$-th number is the $y$-coordinate of the end point of route $i$. The fourth line contains a non-negative integer $k$, the number of guests. The next $k$ lines each contain three non-negative integers $p_i, q_i, r_i$, representing the $x$-coordinate, $y$-coordinate, and observation range of guest $i$. The input also imposes some limits on the total number of intersection points of all routes (segments) between the lines $x = x_{st}$ and $x = x_{ed}$. See “Constraints and Hint” for details.

Output only one line containing two integers: the minimum and maximum possible total scores of the whole aerobatic show, separated by a space.

### Sample 1 Explanation The routes in this sample are exactly those shown in the figure in the statement, except that the guests’ positions are slightly different. The minimum-score plan uses the “head-on swap” stunt at all intersection points, with score $4a + 3c = 13$. The maximum-score plan is the same as the one shown in the figure in the statement, with score $2a + 2b + 3c = 15$. ### Constraints No three or more segments intersect at the same point. All coordinates and $r_i$ are non-negative integers not exceeding $5 \times 10^7$. $y_{i,0} < y_{i + 1,0}$, and all $y_{i,1}$ are distinct. $x_{st} < p_i < x_{ed}, 1 \le a, b, c \le 10^3$. |Test Point ID|Scale of $n, k$|Scale of number of intersections|Notes| |:-:|:-:|:-:|:-:| |$1$|$n, k \le 15$|$\le 40$|None| |$2$|$n, k \le 15$|$\le 40$|None| |$3$|$n, k \le 15$|$\le 40$|None| |$4$|$n, k \le 15$|$\le 40$|None| |$5$|$n \le 30,000, k \le 100$|$\le 200,000$|None| |$6$|$n \le 30,000, k \le 100$|$\le 200,000$|None| |$7$|$n \le 30,000, k \le 100$|$\le 200,000$|None| |$8$|$n \le 30,000, k \le 100$|$\le 200,000$|None| |$9$|$n, k \le 100,000$|$\le 500,000$|$a = b$| |$10$|$n, k \le 100,000$|$\le 500,000$|$a = b$| |$11$|$n, k \le 100,000$|$\le 500,000$|$a = b$| |$12$|$n, k \le 100,000$|$\le 500,000$|$a = b$| |$13$|$n, k \le 50,000$|$\le 250,000$|None| |$14$|$n, k \le 50,000$|$\le 250,000$|None| |$15$|$n, k \le 50,000$|$\le 250,000$|None| |$16$|$n, k \le 50,000$|$\le 250,000$|None| |$17$|$n, k \le 100,000$|$\le 500,000$|None| |$18$|$n, k \le 100,000$|$\le 500,000$|None| |$19$|$n, k \le 100,000$|$\le 500,000$|None| |$20$|$n, k \le 100,000$|$\le 500,000$|None| Translated by ChatGPT 5