P5303 [GXOI/GZOI2019] Forcing OCD to Death

ITX351 wants to pave a $2 \times N$ road, so he bought $N$ $2 \times 1$ bricks. However, one brick cracked in the middle during transportation and became two $1 \times 1$ blocks. This gave ITX351 an evil idea: he wants to deliberately place the two $1 \times 1$ blocks separately on the road, **making sure the two blocks do not share any adjacent edge**. The other bricks can be placed in any way, until the whole road is fully covered. This will surely drive his own OCD (sea5) crazy! Maybe you have already guessed what happens next—he got so excited that he could not type anymore. So he asks you to help compute how many different ways there are to make his plot succeed.

Each test point contains multiple test cases. The first line of the input file is a positive integer $T$, which denotes the number of test cases. Note that different test cases are independent. The next $T$ lines each contain a positive integer $N$, representing the length of the road in that test case.

The output should contain $T$ lines. For each test case, output a positive integer, representing the number of valid tilings that satisfy the condition. Since the answer may be very large, you only need to output the result modulo $1000000007 (10^9 + 7)$.

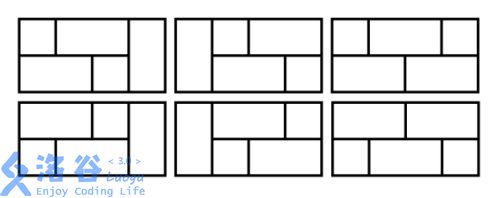
For the sample, the explanation for $N = 4$ is shown in the figure below:  ### Constraints |Test point ID|Scale of $N$|Scale of $T$| |:-:|:-:|:-:| |$1$|$N \le 10$|$T \le 10$| |$2$|$N \le 10$|$T \le 10$| |$3$|$N \le 10^5$|$T \le 50$| |$4$|$N \le 10^5$|$T \le 50$| |$5$|$N \le 10^5$|$T \le 50$| |$6$|$N \le 2 \times 10^9$|$T \le 50$| |$7$|$N \le 2 \times 10^9$|$T \le 50$| |$8$|$N \le 2 \times 10^9$|$T \le 50$| |$9$|$N \le 2 \times 10^9$|$T \le 500$| |$10$|$N \le 2 \times 10^9$|$T \le 500$| Translated by ChatGPT 5