P5305 [GXOI/GZOI2019] Old Words

> Life is but three thousand dreamlike scenes. > I have searched a thousand miles, yet poetry and wine are barren. > I only pour out my ideals in vain, > Better to return home early. > > Warm a pot of dusty-world wine, > Drink alone as the past stretches far away. > Raise the cup and think lightly, > Tears surge like tides, black hair left in a distant land. > > — Wuzhaoshou / Yuqing, "Old Words" You have already solved five problems. Now, under this big tree, you may as well sing an old song to express your feelings. The last problem is about this tree, and its description is very simple. Given a rooted tree with $n$ nodes, with nodes labeled $1 \sim n$, and node $1$ as the root. Given a constant $k$. Given $Q$ queries, each query provides $x, y$. Compute: $$\sum\limits_{i \le x} \text{depth}(\text{lca}(i,y))^k$$ $\text{lca}(x,y)$ denotes the lowest common ancestor of nodes $x$ and $y$ in the rooted tree. $\text{depth}(x)$ denotes the depth of node $x$, where the root has depth $1$. Since the answer may be very large, you only need to output the result modulo $998244353$.

The input contains $n+Q$ lines. Line $1$ contains three positive integers $n, Q, k$. For lines $i = 2 \sim n$, each line contains a positive integer $f_i(1 \le f_i \le n)$, which denotes the label of the parent of node $i$. Next come $Q$ lines, each containing two positive integers $x, y(1 \le x,y \le n)$, representing one query.

The output contains $Q$ lines, each with one integer, which is the answer modulo $998244353$.

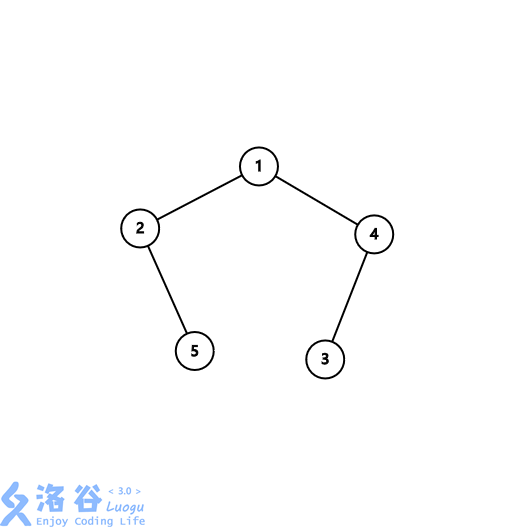
### Sample Explanation The tree in the input:  The depths of the nodes are $1,2,3,2,3$, respectively. For the first query $x = 4, y = 3$, it is easy to compute: $$\text{lca}(1, 3) = 1,\text{lca}(2, 3) = 1,\text{lca}(3, 3) = 3,\text{lca}(4, 3) = 4$$ So $\text{depth}(1)^2+\text{depth}(1)^2+\text{depth}(3)^2+\text{depth}(4)^2 = 1+1+9+4 = 15$. ### Constraints |Test Point ID|Size of $n$|Size of $Q$|Size of $k$|Note| |:-:|:-:|:-:|:-:|:-:| |$1$|$n \le 2,000$|$Q \le 2,000$|$1 \le k \le 10^9$|None| |$2$|$n \le 2,000$|$Q \le 2,000$|$1 \le k \le 10^9$|None| |$3$|$n \le 2,000$|$Q \le 2,000$|$1 \le k \le 10^9$|None| |$4$|$n \le 2,000$|$Q \le 2,000$|$1 \le k \le 10^9$|None| |$5$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|There exists a node whose depth is $n$| |$6$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|There exists a node whose depth is $n$| |$7$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|There exists a node whose depth is $n$| |$8$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|There exists a node whose depth is $n$| |$9$|$n \le 50,000$|$Q = n$|$1 \le k \le 10^9$|For the $i$-th query, $x = i$| |$10$|$n \le 50,000$|$Q = n$|$1 \le k \le 10^9$|For the $i$-th query, $x = i$| |$11$|$n \le 50,000$|$Q \le 50,000$|$k = 1$|None| |$12$|$n \le 50,000$|$Q \le 50,000$|$k = 1$|None| |$13$|$n \le 50,000$|$Q \le 50,000$|$k = 2$|None| |$14$|$n \le 50,000$|$Q \le 50,000$|$k = 2$|None| |$15$|$n \le 50,000$|$Q \le 50,000$|$k = 3$|None| |$16$|$n \le 50,000$|$Q \le 50,000$|$k = 3$|None| |$17$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|None| |$18$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|None| |$19$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|None| |$20$|$n \le 50,000$|$Q \le 50,000$|$1 \le k \le 10^9$|None| Translated by ChatGPT 5