P5319 [BJOI2019] Arcane Staff.

The war on the continent of Bezorath against the disaster legion has reached a stalemate. The elves who have lived on Bezorath for generations began searching for ancient artifacts left by the gods, hoping to use their mysterious power to defeat the disaster legion. After paying a painful price, the elves retrieved a well-preserved staff from a perilous ancient battlefield. However, after the “Twilight of the Gods War”, which all history books consider taboo, the arcane gems inlaid on the staff were already damaged, and its divine power was almost completely exhausted. The elf leaders decided, in the Supreme Council, to mobilize the whole nation to collect the remaining arcane gems, and offered a huge reward to craftsmen across the land to repair the staff. As the 501st inheritor of the divine arts lineage, you have accepted this difficult and sacred mission. From left to right, the staff has $n$ arcane gems inlaid. There are $10$ types of arcane gems, represented by the digits "`0123456789`". Some positions are already damaged, represented by "`.`". You need to fill every damaged position using intact arcane gems (the number of each type is unlimited, and you are not allowed to replace gems that are not damaged). An ancient spellbook records $m$ spells $(S_i, V_i)$, where $S_i$ is a non-empty digit string, and $V_i$ is the divine power that this combination can trigger. The initial divine power of the staff is $Magic = 1$. Whenever the staff contains a consecutive segment of gems equal to $S_i$, the divine power $Magic$ is multiplied by $V_i$. But if the staff contains too many spells, it becomes impure and its power decreases: let $c$ be the number of spells contained in the staff (if the spell type is the same but appears at different positions, it is counted multiple times). The final divine power of the staff is $\sqrt[c]{Magic}$. (If $c = 0$, then the final divine power of the staff is $1$.) For example, if there are two spells $(01, 3)$ and $(10, 4)$, then the divine power of the staff "`0101`" is $\sqrt[3]{3 \times 4 \times 3}$. You need to maximize the final divine power of the repaired staff, and output any one solution.

The first line contains two positive integers $n$ and $m$, representing the number of gems and the number of spells. The second line contains a string $T$ of length $n$, representing the initial staff. The next $m$ lines each contain a non-empty digit string $S_i$ and a positive integer $V_i$, representing each spell.

Output the gems inlaid on the final staff from left to right. If there are multiple solutions, output any one.

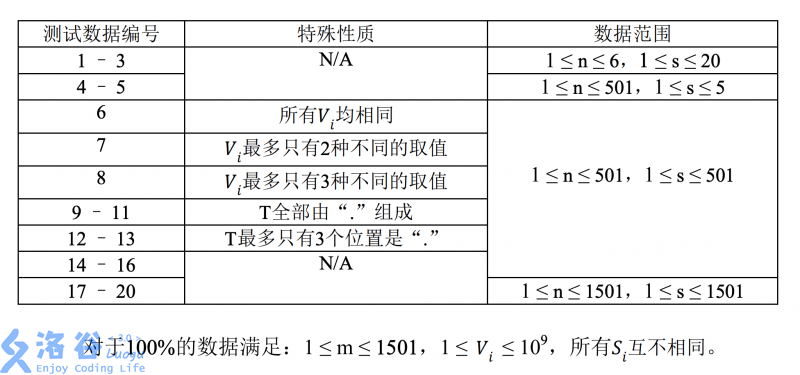
Sample 1: the final divine power of the staff is $2$. Sample 2: the final divine power of the staff is $\sqrt[3]{2 \times 3 \times 4}$. Let $s = \sum_{i=1}^{m} |S_i|$, i.e. the sum of the lengths of all spell strings.  Translated by ChatGPT 5