P5320 [BJOI2019] Seeing Through the Secrets of the Divine Mechanism

The strategist of the Geocast Legion, Black Robe, learned information about the Divine Staff from spies infiltrating the upper ranks of the elves. He is very interested in the ancient mysterious power contained in the Arcane Gems. He seized several Arcane Gems and ordered you, the chief scientist of the Geocast Legion, to lead your researchers to crack them with full effort. After a month of hard work, your team finally deciphered the internal energy structures of the “`2`-type” Arcane Gem and the “`3`-type” Arcane Gem. These two kinds of structures share some similarities. Each gem contains $k$ reaction cores. Each core of a “`2`-type” Arcane Gem can be seen as a $2 \times n$ grid, and each core of a “`3`-type” Arcane Gem can be seen as a $3 \times n$ grid. (Note that $k$ and $n$ may be different for different gems.) When the divine reaction happens, each core is automatically filled with divine particles. Formally, each divine particle can be viewed as a $1 \times 2$ domino placed horizontally or vertically. A core is considered filled if every cell of the grid is covered by exactly one domino. If, between two filling plans, there exists at least one domino whose position or orientation is different, then the two plans are considered different. For example, there are $5$ different ways to fill a $2 \times 4$ grid, and $3$ different ways to fill a $3 \times 2$ grid.  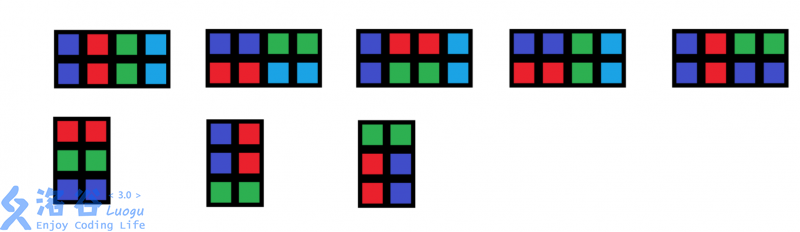If the filling plans of the $k$ cores in an Arcane Gem are all different from each other, they will combine into a powerful spell. Black Robe wants to know how many different spells a gem can produce. (For two spell combinations, if for every core filling plan $a$ in the first combination, one can find some core filling plan $b$ in the second combination such that $a$ and $b$ are exactly the same, then these two spell combinations are considered the same.) For a “`2`-type” Arcane Gem with width $n$ and $k$ reaction cores, let the number of different spells be $F(n,k)$. For a “`3`-type” Arcane Gem with width $n$ and $k$ reaction cores, let the number of different spells be $G(n,k)$. For example, $F(4,1) = 5$, $F(4,2) = 10$, and $G(2,2) = 3$. The Geocast Legion’s technology cannot precisely measure the core length $n$, and can only determine an approximate range $[l,r]$. You need to compute the average number of spells when the core length is within this interval, namely: $$ans2 = \frac{1}{r-l+1}\sum_{n=l}^{r} F(n,k)$$ $$ans3 = \frac{1}{r-l+1}\sum_{n=l}^{r} G(n,k)$$ Let the final answer be in the form $\frac{A}{B}$. Output $A \times B^{-1} \bmod 998244353$, where $B^{-1}$ is the multiplicative inverse of $B$ modulo $998244353$.

The first line contains two positive integers $T$ and $m$, representing the number of test cases and the type of Arcane Gem (only $2$ or $3$). The next $T$ lines each contain three positive integers $l, r, k$, representing the range of core lengths and the number of cores.

For each test case, if $m = 2$ output $ans2$; if $m = 3$ output $ans3$.

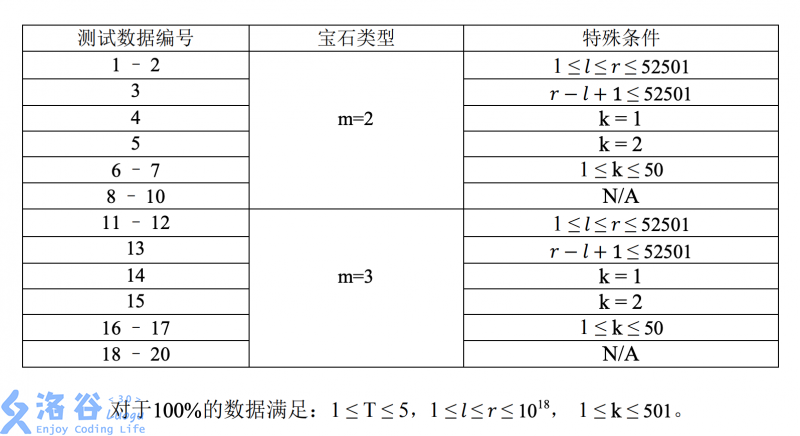
 For all testdata, it is guaranteed that $r-l+1$ is not a multiple of $998244353$. Because the computers in the contest were very slow, after the setter modified the testdata, all cases have $T = 1$. Note: The Constraints of this problem are incorrect. The actual constraints satisfy $1\leq l\leq r\leq 6\times 10 ^ {18}$. Translated by ChatGPT 5