P5321 [BJOI2019] Farewell

Falo is a girl who is afraid of the dark. It is evening. The academic conference that Falo attended has already ended. Lise also finished class and came to pick Falo up to go to the train station. However, the teaching building suddenly lost power, and Falo was surrounded by darkness. Luckily, Lise has already arrived on the same floor of the teaching building. But because the structure of the building is too complex, they can no longer remember the exact layout of this floor. The teaching building in Lise's school has a very regular layout on each floor. Formally, the planar layout of one floor can be drawn on a 2D plane inside the sub-rectangle with $(0,0)$ as the upper-left corner and $(n,m)$ as the lower-right corner (denoted as the rectangle $(0,0) - (n,m)$). The four sides of this sub-rectangle are the outer walls of the building (i.e. four wall segments that are guaranteed to exist). **Note that the coordinate system in this problem is different from the standard Cartesian coordinate system: $(0,0)$ is the upper-left corner and $(n,m)$ is the lower-right corner. $(i,j)$ denotes the vertex in the $(i+1)$-th row and $(j+1)$-th column, not the point with x-coordinate $i$ and y-coordinate $j$.** Each wall segment (an impassable part) is a line segment with endpoints $(i,j)$ and $(i',j')$, denoted as the wall $(i,j) - (i',j')$, where $|i-i'| + |j-j'| = 1$, and $i,i'$ are integers in $[0,n]$, while $j,j'$ are integers in $[0,m]$ (whenever we later use the notation $(i,j) - (i',j')$, we guarantee that all the above conditions are satisfied). Falo knows that for such a layout, there is a method that might allow her to find Lise: Falo places her left hand on the wall, with her arm perpendicular to the wall, and keeps walking forward in this state; at turns she also keeps her left hand on the wall. By doing so, she can walk around one loop and may meet Lise.  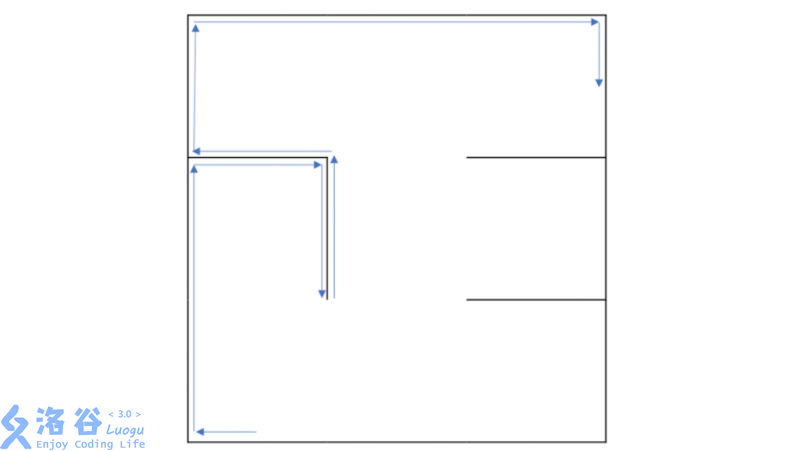The figure above shows Falo's walking route for the first query in the sample input. During the walk, Falo's left hand must stay in contact with the wall. Initially, Falo gives you the initial structure (of this floor) that needs to be maintained, and then there will be $q$ requests. - Operation 1: input format $1 \ x_0 \ y_0 \ x_1 \ y_1$. Falo requests to add a wall segment $(x_0,y_0) - (x_1,y_1)$ to the current structure. It is guaranteed that this wall did not exist before, and it is not on the four sides of the rectangle $(0,0) - (n,m)$. - Operation 2: input format $2 \ x_0 \ y_0 \ x_1 \ y_1$. Falo requests to delete a wall segment $(x_0,y_0) - (x_1,y_1)$ from the current structure. It is guaranteed that this wall existed before, and it is not on the four sides of the rectangle $(0,0) - (n,m)$. - Operation 3: input format $3\ x_0 \ y_0 \ x_1\ y_1\ d_0 \ x_2 \ y_2 \ x_3 \ y_3 \ d_1$. Falo is currently at the midpoint of the wall $(x_0,y_0) - (x_1,y_1)$, i.e. $\left(\frac{x0+x1}{2},\frac{y_0 + y_1}{2}\right)$. $d_0$ is an integer in $[0,1]$ describing which side of the wall Falo is on: $d_0 = 0$ means Falo is on the left/upper side of the wall, and $d_0 = 1$ means on the right/lower side. Lise is currently at the midpoint of the wall $(x_2,y_2) - (x_3,y_3)$, i.e. $\left(\frac{x2+x3}{2},\frac{y_2+y_3}{2}\right)$. The meaning of $d_1$ is the same as $d_0$. It is guaranteed that both wall segments $(x_0,y_0) - (x_1,y_1)$ and $(x_2,y_2) - (x_3,y_3)$ exist, and both positions of Falo and Lise are strictly inside the rectangle $(0,0) - (n,m)$. Compute how much total length Falo needs to walk to find Lise using the method described above (the length of a wall segment $(i,j) - (i',j')$ is $1$, and the length of a half wall segment (since both the start and end are at midpoints) is $\frac{1}{2}$).

There are a total of $2n+q$ lines of input. The first line contains three integers $n$, $m$, $q$, with meanings as described above. The next $n$ lines each contain $m-1$ integers in $[0,1]$. The integer in row $i$ and column $j$ is $1$ if the segment $(i,j) - (i-1,j)$ has a wall, and $0$ otherwise. The next $n-1$ lines each contain $m$ integers in $[0,1]$. The integer in row $i$ and column $j$ is $1$ if the segment $(i,j) - (i,j-1)$ has a wall, and $0$ otherwise. The next $q$ lines each describe one operation, in the format given above.

For each query, output the total length Falo needs to walk to find Lise using the method described above. **If Falo cannot find Lise using the method described above, output $-1$.**

For 10% of the data, $5 \le n,m \le 50$, $1 \le q \le 2000$. For another 30% of the data, there is no operation of type 1. For another 30% of the data, it is guaranteed that at any time, if Falo and Lise stand at any valid positions given by the input format, then Falo can meet Lise. For 100% of the data, $5 \le n,m \le 500$, $1 \le q \le 2 \times 10^5$. Translated by ChatGPT 5