P5323 [BJOI2019] Light Ray

When a beam of light hits a layer of glass, a certain proportion of the light will pass through the glass, a certain proportion will be reflected back, and the rest will be absorbed by the glass. Suppose for any $x$, $x \times a_i\%$ units of light will pass through it, and $x \times b_i\%$ will be reflected back. Now there are $n$ layers of glass stacked together. If $1$ unit of light hits the $1$st layer of glass, how many units of light can pass through **all** $n$ layers of glass?

The first line contains a positive integer $n$, representing the number of glass layers. The next $n$ lines each contain two non-negative integers $a_i, b_i$, representing the transmittance and reflectance of the $i$-th layer.

Output one line containing one integer, representing the amount of light that passes through all the glass layers modulo $10^9 + 7$. It can be proven that the answer must be a rational number. Let the answer be $a/b$ (where $a$ and $b$ are coprime positive integers). If the value you output is $x$, you need to ensure that $a \equiv bx \space (\text{mod }10^9 + 7)$.

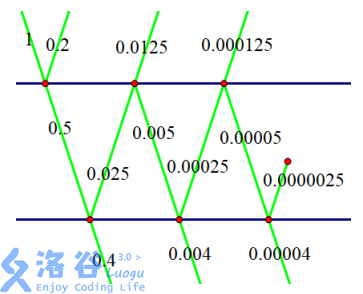
**Explanation for Sample 1:**  As shown in the figure, the light ray enters from the upper-left corner. There are $0.5$ units of light passing through the $1$st layer of glass, and $0.2$ units of light being reflected back. Of these $0.5$ units of light, $0.4$ units pass through the $2$nd layer of glass, and $0.025$ units of light are reflected back. Of these $0.025$ units of light, $0.0125$ units pass through the $1$st layer of glass, and $0.005$ units of light are reflected back. Of these $0.005$ units of light, $0.004$ units pass through the $2$nd layer of glass... Therefore, the total amount of light passing through the two layers of glass is $0.40404... = 40/99$ units. Modulo $10^9+7$, this equals $858585865$. **Constraints:** For $5\%$ of the testdata, $n=1$; For $20\%$ of the testdata, $n \le 2$; For $30\%$ of the testdata, $n \le 3$; For $50\%$ of the testdata, $n \le 100$; For $70\%$ of the testdata, $n \le 3000$; For $100\%$ of the testdata, $n \le 5\times 10^5$, $1 \le a_i \le 100$, $0 \le b_i \le 99$, $1 \le a_i+b_i \le 100$. In each group, $a_i$ and $b_i$ are generated randomly among integers that satisfy the above constraints. Translated by ChatGPT 5