P5324 [BJOI2019] 删数

对于任意一个数列，如果能在有限次进行下列删数操作后将其删为空数列，则称这个数列可以删空。一次删数操作定义如下： >记当前数列长度为 $k$ ，则删掉数列中所有等于 $k$ 的数。 现有一个长度为 $n$ 的数列 $a$，有 $m$ 次修改操作，第 $i$ 次修改后你要回答： 经过 $i$ 次修改后的数列 $a$，至少还需要修改几个数才可删空？ 每次修改操作为单点修改或数列整体加一或数列整体减一。

第一行两个正整数 $n,m$，分别表示数列长度、修改次数。 第二行有 $n$ 个正整数，表示数列 $a$，即输入的第 $i$ 个数表示数列 $a$ 的第 $i$ 个数 $a_i$。 接下来 $m$ 行，每行两个整数 $p,x$，表示一次修改操作。 当 $1\le p \le n$ 时，该操作为单点修改，将数列中第 $p$ 个数 $a_p$ 修改为 $x$ 当 $p=0$ 时，该操作为数列整体加 $x$。

输出 $m$ 行，每行一个整数，第 $i$ 行表示前 $i$ 次修改后的答案。

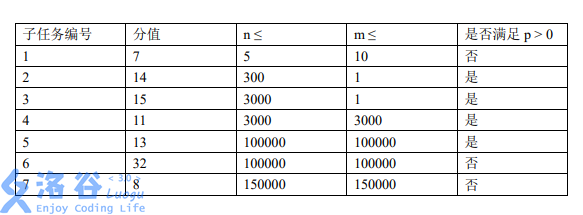
**样例解释(局部)：** 第一次修改后，数列为 $(1, 2, 3)$，无需修改即可删空。 第四次修改后，数列为 $(4, 5, 6)$，需要将三个数都改掉才可能删空。 第六次修改后，数列为 $(4, 2, 2)$，将第一个数改成 $3$ 即可删空。 第九次修改后，数列为 $(1, -1, -1)$，可以将第二个数改成 $2$、第三个数改成 $3$ 来删空。 **数据范围：** 对于 $100\%$ 的数据： - $1\le n,m \le 150000, 1\le a_i \le n, 0\le p\le n$ - $p>0$ 时，$1\le x \le n$ - $p=0$ 时，$x\in \{-1, 1\}$