P5324 [BJOI2019] Deleting Numbers

For any sequence, if it can be deleted into an empty sequence after performing the following delete operation a finite number of times, then the sequence is said to be deletable to empty. One delete operation is defined as follows: > Let the current sequence length be $k$. Then delete all numbers in the sequence that are equal to $k$. Now there is a sequence $a$ of length $n$, and there are $m$ modification operations. After the $i$-th modification, you need to answer: For the sequence $a$ after $i$ modifications, what is the minimum number of elements that still need to be changed so that it can be deleted to empty? Each modification is either a point update, or adding $1$ to the whole sequence, or subtracting $1$ from the whole sequence.

The first line contains two positive integers $n, m$, representing the sequence length and the number of modifications. The second line contains $n$ positive integers, representing the sequence $a$. That is, the $i$-th input number is the $i$-th element of the sequence, $a_i$. The next $m$ lines each contain two integers $p, x$, representing one modification operation. When $1 \le p \le n$, this operation is a point update: set the $p$-th number in the sequence, $a_p$, to $x$. When $p = 0$, this operation adds $x$ to the whole sequence.

Output $m$ lines, each containing one integer. The $i$-th line denotes the answer after the first $i$ modifications.

**Sample Explanation (partial):** After the first modification, the sequence is $(1, 2, 3)$, and it can be deleted to empty without any changes. After the fourth modification, the sequence is $(4, 5, 6)$, and all three numbers must be changed before it can possibly be deleted to empty. After the sixth modification, the sequence is $(4, 2, 2)$, and changing the first number to $3$ makes it deletable to empty. After the ninth modification, the sequence is $(1, -1, -1)$, and you can change the second number to $2$ and the third number to $3$ to make it deletable to empty. 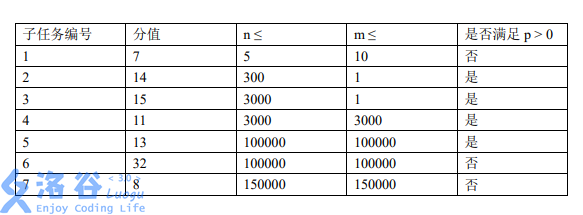**Constraints:** For $100\%$ of the testdata: - $1 \le n, m \le 150000$, $1 \le a_i \le n$, $0 \le p \le n$. - When $p > 0$, $1 \le x \le n$. - When $p = 0$, $x \in \{-1, 1\}$.  Translated by ChatGPT 5