P5332 [JSOI2019] Accurate Prediction

JYY and his Mars exploration team have landed in the Mars town again. They plan to teach the Martians knowledge about machine learning to improve their life efficiency. However, the Martians, with limited intelligence, say they do not believe in computer science. To fully convince them, JYY's team found detailed historical records about Mars and trained a prediction model. This model can accurately predict whether Martians will live or die in the future.

Currently, there are $n$ residents in the Mars town (numbered $1,2,\ldots,n$). A machine learning algorithm predicts the life-or-death status of these residents over the next $T$ moments (numbered $1,2,\ldots,T$). Each prediction is one of the following two types: - Brothers in Misfortune $0$ $t$ $x$ $y$: At moment $t$, if $x$ is dead, then at moment $t+1$, $y$ is dead. (Note that if $x$ is alive at moment $t$, this prediction is also considered correct.) - Death God Arrives $1$ $t$ $x$ $y$: At moment $t$, if $x$ is alive, then at moment $t$, $y$ is dead. (Note that if $x$ is dead at moment $t$, this prediction is also considered correct.) Note that this problem is predicting the life-or-death status at a specific moment. If someone is alive at moment $t$ and dead at moment $t+1$, you may assume that some event happened during the time interval from $t$ to $t+1$ that caused their death. Although JYY is very confident in the model obtained from big data statistics, the Martians are shocked by these predictions and feel it is hard to accept such a setting. They even think computer science is a scary cult that has broken their peaceful life. To calm the Martians down, JYY plans to derive some facts from these prediction results that are easier for the Martians to accept. Specifically, JYY first assumes that all predictions about the Martians' life and death are correct. Based on this, JYY wants to compute, for each resident $k$, how many Martians might be able to live together with him until moment $T+1$. In other words, for each Martian $k$, JYY wants to compute $$\sum_{1 \leq i \leq n,i \neq k} \operatorname{Live}(k,i)$$ where $\operatorname{Live}(i,j)=1$ means that Martians $i$ and $j$ may possibly both be alive at moment $T+1$; otherwise, $\operatorname{Live}(i,j)=0$. Note that Martians cannot be resurrected. A Martian may already be dead at moment $1$, and there may also be deaths not covered by any prediction (a Martian can die at any time, but at any moment, a Martian's observed state is either alive or dead). Finally, note that $\operatorname{Live}$ is computed independently for each pair of Martians, so $\operatorname{Live}(x,y)=1$ and $\operatorname{Live}(y,z)=1$ does not imply $\operatorname{Live}(x,z)=1$.

The first line contains three integers $T,n,m$. The next $m$ lines each describe a prophecy. The first integer $c$ of each prophecy indicates its type: - $c=0$: then read $t,x,y$; - $c=1$: then read $t,x,y$.

Output $n$ numbers as the answers, separated by spaces.

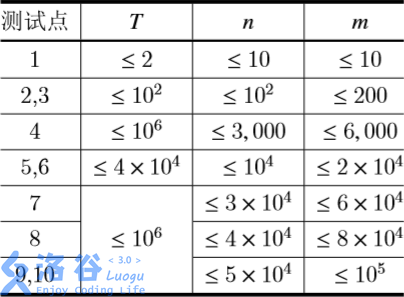
 Translated by ChatGPT 5