P5333 [JSOI2019] Neural Network

The Mars exploration team discovered that Martians think very differently from humans because they have a very different neural network structure. To better understand Martian behavior patterns, JYY scanned the brains of Martians in a small town and obtained some important data.

After a Martian is born, its neural network can be seen as a forest consisting of several undirected trees $\{T_1(V_1, E_1), T_2(V_2, E_2),\ldots T_m(V_m, E_m)\}$. As the Martian grows older, the number of neural connections keeps increasing. Initially, the set of newly grown connections in the neural network is $E^\ast = \varnothing$. The neural network grows according to the following rule: - If nodes $u \in V_i$ and $v \in V_j$ belong to different undirected trees $T_i$ and $T_j$ respectively ($i \neq j$), then $E^\ast$ should contain the edge $(u, v)$. Finally, after no more neural network connections can grow, the connections between nodes in the neural network can be regarded as an undirected graph $G(V,E)$, where $$V=V_1\cup V_2\cup \ldots \cup V_m,E=E_1\cup E_2\cup \ldots \cup E_m\cup E^\ast$$ Martians make decisions by creating cycles in $G(V, E)$. For different external inputs, Martians will create different neural connection cycles and thus produce different responses. To understand how complex Martian behavior patterns are, JYY decides to compute the **number of Hamiltonian cycles in $G$**. A Hamiltonian cycle of $G(V, E)$ is a simple cycle that starts from the first node of the first tree, visits every other node in $V$ exactly once, and then returns to the first node of the first tree.

The first line contains $m$, the number of undirected trees in the Martian neural network at the beginning. Then there are $m$ parts, where the $i$-th part describes the tree $T_i$. For $T_i$, the first line contains $k_i$, the number of nodes in the tree $T_i(V_i, E_i)$. Assume $V_i = \{v_1, v_2,\ldots ,v_{k_i}\}$. In the next $k_i - 1$ lines, each line contains two integers $x, y$, meaning there is a tree edge between nodes $v_x$ and $v_y$ ($1 \le x, y \le k_i$), i.e., $(v_x, v_y) \in E_i$.

Since the number of Hamiltonian cycles can be very large, output a non-negative integer equal to the answer modulo $998244353$.

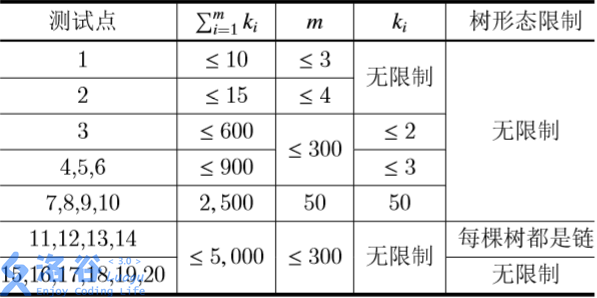
 Translated by ChatGPT 5