P5347 [XR-1] Tetris

Xiao Fen Tu has recently become addicted to a game called “Tetris”. However, this problem has almost nothing to do with Tetris except that they both have grids and colors.

There is an $n \times m$ grid. Xiao Fen Tu plans to draw lines in it. He may draw lines any number of times, or draw none. Each time he draws, he must start from the center of a cell that has not been drawn before. He may draw only in four directions: up, down, left, and right. The cell in the chosen direction is called the **target cell**. The target cell can be drawn if and only if one of the following three cases holds: 1. If the target cell **has not been drawn**, then he may pass through the midpoint of the common edge of the two cells and draw directly to the center of the target cell. In this case, he **may choose** to end this drawing operation. 2. If the target cell **has been drawn**, and the drawn line is a **line that goes through the entire cell**, then he may draw another **line that goes through the entire cell** that is **perpendicular** to the existing one. A **line that goes through the entire cell** is defined as a line that **does not change direction** inside the cell, and goes through it **from top to bottom** or **from left to right**. 3. If the target cell is the **starting cell** of the current drawing operation, then he may pass through the midpoint of the common edge of the two cells and draw directly to the center of the target cell. In this case, he **must** end this drawing operation. Of course, he cannot draw outside the whole grid. Even with such strict rules, he still has many colors of pens. Each time he draws, he may choose any one of the $c$ colors to draw the line. Unfortunately, some positions in the grid are broken and cannot be passed through, meaning that in any drawing operation he cannot draw onto broken positions. Xiao Fen Tu wants to know: under these constraints, how many essentially different drawings can be produced in the end? Xiao Fen Tu does not want to be too demanding. When $\mathrm{op}=0$, two drawings are essentially the same if and only if, ignoring the broken cells, they look the same (the line direction and color at each position are the same). When $\mathrm{op}=1$, two drawings are essentially the same if and only if, ignoring the broken cells, they look the same, or they look the same after a $180 ^ {\circ}$ rotation. Since the answer may be very large, you only need the result modulo $998244353$.

The first line contains three positive integers $n,m,c$ and an integer $\mathrm{op}$ that is either $0$ or $1$. Then follow $n$ lines, each containing a string of length $m$ consisting only of `.` and `#`, describing the grid. If the $j$-th character in the $i$-th line is `#`, it means the cell in row $i$, column $j$ is broken; otherwise it is not broken.

Output one line with one number, the answer modulo $998244353$.

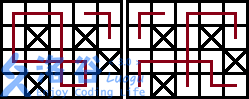
[Sample $1$ Explanation] There are the following $7$ essentially different drawings:  [Sample $6$ Explanation] Two essentially different drawings are given below:  [Data Scale and Constraints] This problem uses bundled testdata: Subtask 1 (12 points): $n=1$, $\mathrm{op}=0$, with no broken cells. Subtask 2 (13 points): $c=1$, $\mathrm{op}=0$. Subtask 3 (12 points): $c=1$, $\mathrm{op}=1$. Subtask 4 (14 points): $m\le 5$, $\mathrm{op}=0$. Subtask 5 (25 points): $\mathrm{op}=0$. Subtask 6 (8 points): $n\bmod 2=0$, $\mathrm{op}=1$. Subtask 7 (8 points): $n\bmod 2=1$, $m\bmod 2=0$, $\mathrm{op}=1$. Subtask 8 (8 points): $n\bmod 2=1$, $m\bmod 2=1$, $\mathrm{op}=1$. For $100\%$ of the data, $1\le n,m\le 9$, $1\le c\le 10^6$, $\mathrm{op}\in\{0,1\}$。 Translated by ChatGPT 5