P5380 [THUPC 2019] Duck Chess.

#### Background Duck Chess is a board game that is popular among ducks. In fact, it is somewhat similar to Chinese Chess, but the rules are not exactly the same. Here, we will introduce the rules of Duck Chess. **At the same time, we provide a toy that simulates the rules of Duck Chess. You can use this toy to better understand the problem** (you may also play with your teammates after getting AK). For details, see “Toy Instructions”. Duck Chess is played on a $10\times 9$ grid board ($10$ rows and $9$ columns). Each grid point can hold a piece. One player uses the red (`red`) pieces, and the other uses the blue (`blue`) pieces. The two players take turns to make moves. When it is a player’s turn, they must choose one of their own pieces and make exactly one move according to the rules. 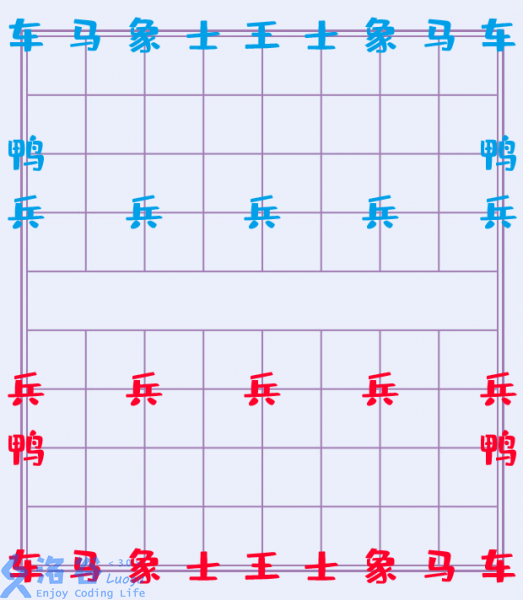The inventor Duck De规定 (De Guiding, “规定”) specified that red moves first, and designed the initial board layout as follows:  ##### Piece Types and Moving Rules There are $7$ types of pieces. Below are their names and moving rules. When describing moving rules, we assume the piece is at position $\left(x,y\right)$ (meaning row $x$, column $y$, same below), and list the positions it can reach: * **Captain** (`captain`): It can reach $4$ positions, including $\left(x\pm 1,y\right)$ and $\left(x,y\pm 1\right)$. * **Guard** (`guard`): It can reach $4$ positions, including $\left(x\pm 1,y\pm 1\right)$ and $\left(x\pm 1,y\mp 1\right)$. * **Elephant** (`elephant`): It can reach at most $4$ positions. For any $s_x,s_y\in \left\{ 1,-1\right\}$: * If there is **no piece of either side** on $\left(x+s_x\times 1 ,y+ s_y\times 1\right)$, then $\left( x+s_x \times 2,y+s_y \times 2\right)$ is a reachable position. * **Horse** (`horse`): It can reach at most $8$ positions. For any $s_x,s_y\in \left\{ 1,-1\right\}$: * If there is **no piece of either side** on $\left(x+s_x\times 1 ,y\right)$, then $\left( x+s_x \times 2,y+s_y \times 1\right)$ is a reachable position. * If there is **no piece of either side** on $\left(x ,y+ s_y \times 1 \right)$, then $\left( x+s_x \times 1,y+s_y \times 2\right)$ is a reachable position. * **Car** (`car`): Without **jumping over other pieces**, it can reach all other positions in the same row or the same column. * **Duck** (`duck`): It can reach at most $8$ positions. For any $s_x,s_y\in \left\{ 1,-1\right\}$: * If both $\left(x+s_x\times 2 ,y+s_y \times 1\right)$ and $\left(x+s_x\times 1 ,y\right)$ have **no piece of either side**, then $\left( x+s_x \times 3,y+s_y \times 2\right)$ is a reachable position. * If both $\left(x+s_x \times 1 ,y+ s_y \times 2 \right)$ and $\left(x ,y+ s_y \times 1 \right)$ have **no piece of either side**, then $\left( x+s_x \times 2,y+s_y \times 3\right)$ is a reachable position. * **Soldier** (`soldier`): It can reach $8$ positions, including $\left(x\pm 1,y\right)$ and $\left(x,y\pm 1\right)$ and $\left(x\pm 1,y\pm 1\right)$ and $\left(x\pm 1,y\mp 1\right)$. **In addition to the rules described above, piece movement also follows these extra rules:** * You cannot move a piece to a position outside the board. * A player cannot move a piece to a position that is **already occupied by one of their own pieces**. * If a player moves a piece to a position **occupied by an opponent’s piece**, then that **opponent’s piece** is removed from the game. ##### Winning Condition and “Check” Positions The goal of the game is to remove the opponent’s **captain** from the game. Once a side’s **captain** is removed, the other side wins immediately. For a board state, if one side has a legal move that can remove the other side’s **captain** from the game in one step, then we say the current position is a **check** position. As a friendly reminder, by definition, forming a check position includes (but is not limited to) the following possibilities: 1. Moving a piece to a position where it can attack the opponent’s **captain**. 2. Not taking any action to avoid threats when one’s own **captain** is under threat. 3. Actively moving the **captain** to a position that will be attacked. **In addition, note that after the game ends, since neither side can make any further moves, it is impossible for a check position to exist, even if at that time the other side’s captain is in an “attacked” position.** #### Problem Description This year’s IDCC (International Duck Chess Competition) is in full swing. You watched an amazing match, but your memory of the game process has become blurry. Only the system’s **operation sequence** is left. Each **operation** in the sequence is the current player’s attempt to move a piece from one position to another. You want to use this sequence to reproduce the entire game process. That is, for each operation, you need to **first determine whether it is legal**. If it is legal, then you need to **further determine**: 1. Which piece is moved by this operation. 2. After this operation, whether any piece is removed from the game. If so, also determine which piece is removed. 3. After this operation, whether a check position is formed. 4. After this operation, whether the game ends. Possible illegal situations include: * There is no piece of the current player at the starting position of this move. * There is a piece of the current player at the starting position, but the move does not follow the rules. * The game has already ended. Illegal operations in the sequence should be ignored. For example, if it is red’s turn to move and the current operation in the sequence is illegal, then this operation is ignored, and the next operation in the sequence becomes red’s operation for this turn (if it is still illegal, keep ignoring, until a legal operation appears).

The first line contains a non-negative integer $Q$, indicating the length of the operation sequence. Next, each operation is described in order. In the next $Q$ lines, each line contains $4$ integers $x_s, y_s, x_t, y_t$ ($0\leq x_s,x_t < 10$, $0\leq y_s,y_t < 9$), describing an operation that attempts to move the piece at $\left(x_s,y_s\right)$ to $\left(x_t,y_t\right)$. Here, we define the bottom-left corner (i.e., the position where red’s **car** is placed, see the figure in “Background”) as $\left(0,0\right)$. It is guaranteed that $Q\leq 1000$.

Output $Q$ lines. For each operation, output the reproduction result in order. Each line outputs the result of one operation: * If the operation is illegal, output `Invalid command`. * If it is legal, answer questions $1\sim 4$ in “Problem Description” in order: * Describe the moved piece as `[color] [type]` (note there is a space), using their English names (see “Background”). For example, a red elephant is `red elephant`, and a blue captain is `blue captain`. * The piece removed from the game is described in the same way as above. In particular, **if no piece is removed, the answer to this question is `NA`**. * Use `yes` and `no` to indicate whether a check position is formed. * Use `yes` and `no` to indicate whether the game ends. * Use `;` (semicolon) to separate the answers to all questions. * For example, if the four answers are: the moved piece is a blue car, no piece is removed, a check position is formed, and the game does not end, then the line should be `blue car;NA;yes;no`.

##### Toy Instructions You can run the toy by executing the following command in the directory where the toy is located (link: extract code: 4d5c): ``` ./duckchess ``` In particular, **before the first run**, you need to execute the following command to add execute permission: ``` chmod +x duckchess ``` ##### Copyright Information From THUPC (THU Programming Contest) 2019. Resources such as editorials can be found at . Translated by ChatGPT 5